
【題目】某果園種植“糖心蘋果”已有十余年,根據其種植規模與以往的種植經驗,產自該果園的單個“糖心蘋果”的果徑(最大橫切面直徑,單位:![]() )在正常環境下服從正態分布
)在正常環境下服從正態分布![]() .
.
(1)一顧客購買了20個該果園的“糖心蘋果”,求會買到果徑小于56![]() 的概率;
的概率;
(2)為了提高利潤,該果園每年投入一定的資金,對種植、采摘、包裝、宣傳等環節進行改進.如圖是2009年至2018年,該果園每年的投資金額![]() (單位:萬元)與年利潤增量
(單位:萬元)與年利潤增量![]() (單位:萬元)的散點圖:
(單位:萬元)的散點圖:
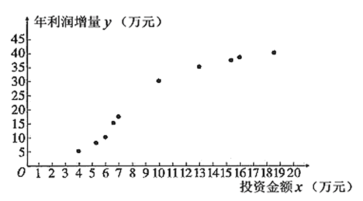
該果園為了預測2019年投資金額為20萬元時的年利潤增量,建立了![]() 關于
關于![]() 的兩個回歸模型;
的兩個回歸模型;
模型①:由最小二乘公式可求得![]() 與
與![]() 的線性回歸方程:
的線性回歸方程:![]() ;
;
模型②:由圖中樣本點的分布,可以認為樣本點集中在曲線:![]() 的附近,對投資金額
的附近,對投資金額![]() 做交換,令
做交換,令![]() ,則
,則![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)根據所給的統計量,求模型②中![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(II)根據下列表格中的數據,比較兩種模型的相關指數![]() ,并選擇擬合精度更高、更可靠的模型,預測投資金額為20萬元時的年利潤增量(結果保留兩位小數).
,并選擇擬合精度更高、更可靠的模型,預測投資金額為20萬元時的年利潤增量(結果保留兩位小數).
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
| 102.28 | 36.19 |
附:若隨機變量![]() ,則
,則![]() ,
,![]() ;樣本
;樣本![]() 的最小乘估計公式為
的最小乘估計公式為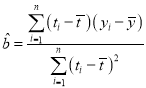 ,
,![]() ;
;
相關指數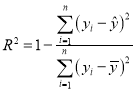 .
.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)0.3695;(2)(I)![]() ,(II)模型①的
,(II)模型①的![]() 小于模型②,說明回歸模型②刻畫的擬合效果更好,當
小于模型②,說明回歸模型②刻畫的擬合效果更好,當![]() 時,模型②的年利潤增量的預測值為
時,模型②的年利潤增量的預測值為![]() (萬元),
(萬元),
【解析】
(1)由已知滿足正態分布,則可知![]() ,
,![]() 的值,由正態分布的對稱性可知,可求得買一個蘋果,其果徑小于56
的值,由正態分布的對稱性可知,可求得買一個蘋果,其果徑小于56![]() 的概率
的概率![]() ,由獨立重復試驗概率的運算方式,求得購買20個“糖心蘋果”中有果徑小于56
,由獨立重復試驗概率的運算方式,求得購買20個“糖心蘋果”中有果徑小于56![]() 的蘋果概率;
的蘋果概率;
(2)(I)由最小二乘法求得模型②中![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(II)分別計算兩種模型的相關系數的平方,得模型②的相關系數的平方更大其擬合程度越好,再代![]() 進行計算,求得預測值.
進行計算,求得預測值.
(1)由已知,當個“糖心蘋果”的果徑![]() ,
,
則![]() ,
,![]() .
.
由正態分布的對稱性可知,
![]() 設一顧客購買了20個該果園的“糖心蘋果”,其中果徑小于56
設一顧客購買了20個該果園的“糖心蘋果”,其中果徑小于56![]() 的有
的有![]() 個,則
個,則![]() ,
,
故![]() ,
,
所以這名顧客所購買20個“糖心蘋果”中有果徑小于56![]() 的蘋果概率為0.3695.
的蘋果概率為0.3695.
(2)(I)由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
又由題,得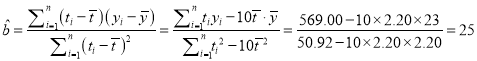 ,
,
則![]()
所以,模型②中![]() 關于
關于![]() 的回歸方程
的回歸方程![]() .
.
(II)由表格中的數據,有![]() ,即
,即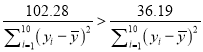 ,
,
所以模型①的![]() 小于模型②,說明回歸模型②刻畫的擬合效果更好,
小于模型②,說明回歸模型②刻畫的擬合效果更好,
當![]() 時,模型②的年利潤增量的預測值為
時,模型②的年利潤增量的預測值為
![]() (萬元),
(萬元),
這個結果比模型①的預測精度更高、更可靠.


科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() .
.
(1)證明:數列![]() 為等差數列;
為等差數列;
(2)設數列![]() 的前n項和為
的前n項和為![]() ,若
,若![]() ,且對任意的正整數n,都有
,且對任意的正整數n,都有![]() ,求整數
,求整數![]() 的值;
的值;
(3)設數列![]() 滿足
滿足![]() ,若
,若![]() ,且存在正整數s,t,使得
,且存在正整數s,t,使得![]() 是整數,求
是整數,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示, ![]() 是邊長為3的正方形,
是邊長為3的正方形, ![]() 平面
平面![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)設點![]() 是線段
是線段![]() 上一個動點,試確定點
上一個動點,試確定點![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并證明你的結論.
,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
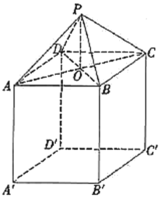
【題目】如圖所示,一個倉庫設計由上部屋頂和下部主體兩部分組成,屋頂的形狀是四棱錐![]() ,四邊形
,四邊形![]() 是正方形,點
是正方形,點![]() 為正方形
為正方形![]() 的中心,
的中心,![]() 平面
平面![]() ;下部的形狀是長方體
;下部的形狀是長方體![]() .已知上部屋頂造價與屋頂面積成正比,比例系數為
.已知上部屋頂造價與屋頂面積成正比,比例系數為![]() ,下部主體造價與高度成正比,比例系數為
,下部主體造價與高度成正比,比例系數為![]() .若欲造一個上、下總高度為10
.若欲造一個上、下總高度為10![]() ,
,![]()
![]() 的倉庫,則當總造價最低時,
的倉庫,則當總造價最低時,![]() ( )
( )
A.![]()
![]() B.
B.![]()
![]() C.4
C.4![]() D.
D.![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中取兩個定點
中取兩個定點![]() ,
,![]() ,再取兩個動點
,再取兩個動點![]() ,
,![]() ,且
,且![]() .
.
(1)求直線![]() 與
與![]() 的交點
的交點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過![]() 的直線與軌跡
的直線與軌跡![]() 交于
交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸且與軌跡
軸且與軌跡![]() 交于另一點
交于另一點![]() ,
,![]() 為軌跡
為軌跡![]() 的右焦點,若
的右焦點,若![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設α是給定的平面,A,B是不在α內的任意兩點,則( )
A.在α內存在直線與直線AB異面
B.在α內存在直線與直線AB相交
C.在α內存在直線與直線AB平行
D.存在過直線AB的平面與α垂直
E.存在過直線AB的平面與α平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左、右兩個頂點分別是A1,A2,左、右兩個焦點分別是F1,F2,P是雙曲線上異于A1,A2的任意一點,給出下列命題,其中是真命題的有( )
的左、右兩個頂點分別是A1,A2,左、右兩個焦點分別是F1,F2,P是雙曲線上異于A1,A2的任意一點,給出下列命題,其中是真命題的有( )
A.![]()
B.直線![]() 的斜率之積等于定值
的斜率之積等于定值![]()
C.使得![]() 為等腰三角形的點
為等腰三角形的點![]() 有且僅有8個
有且僅有8個
D.![]() 的面積為
的面積為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com