
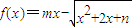 (x∈[-2,+∞),若存在閉區間[a,b]⊆[-2,+∞)(a<b),使得對任意x∈[a,b],恒有f(x)=c(c為實常數),則實數m,n的值依次為 .
(x∈[-2,+∞),若存在閉區間[a,b]⊆[-2,+∞)(a<b),使得對任意x∈[a,b],恒有f(x)=c(c為實常數),則實數m,n的值依次為 .  一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
| -x2+x+2 |
|
| -x2+x+2 |
A、K的最大值為2
| ||
B、K的最小值為2
| ||
| C、K的最大值為1 | ||
| D、K的最小值為1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| π |
| 2 |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| -x2+x+2 |
|
| -x2+x+2 |
A.K的最大值為2
| B.K的最小值為2
| ||||
| C.K的最大值為1 | D.K的最小值為1 |
查看答案和解析>>
科目:高中數學 來源:2009年上海市浦東新區高考數學一模試卷(理科)(解析版) 題型:解答題
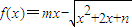 (x∈[-2,+∞),若存在閉區間[a,b]⊆[-2,+∞)(a<b),使得對任意x∈[a,b],恒有f(x)=c(c為實常數),則實數m,n的值依次為 .
(x∈[-2,+∞),若存在閉區間[a,b]⊆[-2,+∞)(a<b),使得對任意x∈[a,b],恒有f(x)=c(c為實常數),則實數m,n的值依次為 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com