
如圖,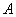 ,
, ,
,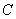 ,
, 四點(diǎn)共圓,
四點(diǎn)共圓,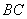 與
與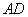 的延長(zhǎng)線交于點(diǎn)
的延長(zhǎng)線交于點(diǎn) ,點(diǎn)
,點(diǎn) 在
在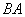 的延長(zhǎng)線上.
的延長(zhǎng)線上.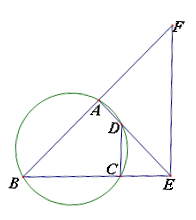
(1)若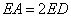 ,
, ,求
,求 的值;
的值;
(2)若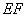 ∥
∥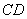 ,求證:線段
,求證:線段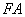 ,
,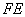 ,
, 成等比數(shù)列.
成等比數(shù)列.
(1) (2)先證
(2)先證 ∽
∽
解析試題分析:(Ⅰ)解:由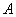 ,
, ,
,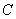 ,
, 四點(diǎn)共圓,得
四點(diǎn)共圓,得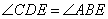 ,
,
又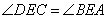 ,∴
,∴ 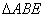 ∽
∽ ,于是
,于是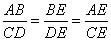 . ①
. ①
設(shè) ,
,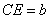 ,則由
,則由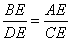 ,得
,得 ,即
,即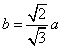
代入①,得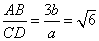 .
.
(Ⅱ)證明:由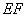 ∥
∥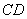 ,得
,得 .
.
∵ 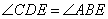 ,∴
,∴ 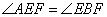 .又
.又 ,
,
∴  ∽
∽ ,于是
,于是 ,故
,故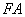 ,
,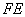 ,
, 成等比數(shù)列.
成等比數(shù)列.
考點(diǎn):圓內(nèi)接多邊形的性質(zhì)與判定;相似三角形的判定;相似三角形的性質(zhì).
點(diǎn)評(píng):本題在圓內(nèi)接四邊形的條件下,一方面證明兩條直線平行,另一方面求線段的比值.著重考查了圓中的比例線段、圓內(nèi)接四邊形的性質(zhì)和相似三角形的判定與性質(zhì)等知識(shí)點(diǎn),屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,在△ABC中,CD是∠ACB的平分線,△ACD的外接圓交于BC于點(diǎn)E,AB=2AC.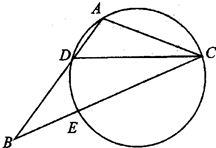
(Ⅰ)求證:BE=2AD;
(Ⅱ)當(dāng)AC=1,EC=2時(shí),求AD的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,已知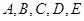 均在⊙O上,且
均在⊙O上,且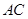 為⊙O的直徑。
為⊙O的直徑。
(Ⅰ)求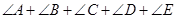 的值;
的值;
(Ⅱ)若⊙O的半徑為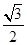 ,
, 與
與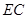 交于點(diǎn)
交于點(diǎn) ,且
,且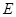 、
、 為弧
為弧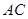 的三等分點(diǎn),求
的三等分點(diǎn),求 的長(zhǎng).
的長(zhǎng).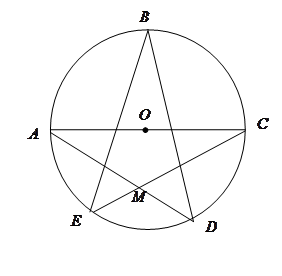
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在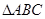 中,AB=AC,過(guò)點(diǎn)A的直線與其外接圓交于點(diǎn)P,交BC延長(zhǎng)線于點(diǎn)D。
中,AB=AC,過(guò)點(diǎn)A的直線與其外接圓交于點(diǎn)P,交BC延長(zhǎng)線于點(diǎn)D。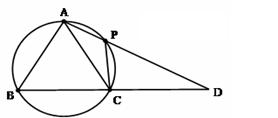
(1)求證: 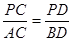 ;
;
(2)若AC=3,求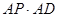 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
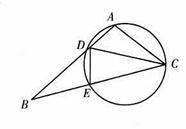
如圖,四邊形 是圓內(nèi)接四邊形,延長(zhǎng)
是圓內(nèi)接四邊形,延長(zhǎng)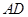 與的延長(zhǎng)線
與的延長(zhǎng)線 交于點(diǎn)
交于點(diǎn)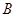 ,且
,且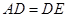 ,
, 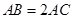 .
.
(1)求證: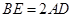 ;
;
(2)當(dāng)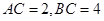 時(shí),求
時(shí),求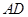 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,直線l與⊙O相切于點(diǎn)A,點(diǎn)P為直線l上一點(diǎn),直線PO交⊙O于點(diǎn)C、B,點(diǎn)D在線段AP上,連結(jié)DB,且AD=DB.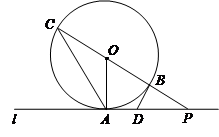
 (1)判斷直線DB與⊙O的位置關(guān)系,并說(shuō)明理由;
(1)判斷直線DB與⊙O的位置關(guān)系,并說(shuō)明理由;
(2)若PB=BO,⊙O的半徑為4cm,求AC的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分10分)選修4-1:幾何證明講 如圖,AB是⊙O的直徑,弦BD、CA的延長(zhǎng)線相交于點(diǎn)E,EF垂直BA的延長(zhǎng)線于點(diǎn)F. 
求證:(1) ;
;
(2)AB2=BE•BD-AE•AC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分10分)選修4-1幾何證明選講
如圖,在 中,
中, ,
,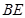 平分
平分 交
交 于點(diǎn)
于點(diǎn) ,點(diǎn)
,點(diǎn) 在
在 上,
上, .
.
(1)求證: 是△
是△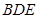 的外接圓的切線;
的外接圓的切線;
(2)若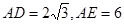 ,求
,求 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com