
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,將
,將![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度后得到函數
個單位長度后得到函數![]() ,
,![]() 的圖像關于
的圖像關于![]() 軸對稱,且
軸對稱,且![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)設函數![]() ,若函數
,若函數![]() 的圖像在
的圖像在![]() 上恰有2個最高點,求實數
上恰有2個最高點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據給出的周期,可求出ω的值;由f(x)的圖象向右平移![]() 個單位長度,函數的圖象關于y軸對稱,求出φ的值;由
個單位長度,函數的圖象關于y軸對稱,求出φ的值;由![]() ,得A的值即可;
,得A的值即可;
(2)由(1)可得F(x)的解析式,由輔助角公式進行化簡,利用函數圖象分析即可得出結果.
(1)∵函數![]() 的最小正周期為π,
的最小正周期為π,
∴π![]() ,解得ω=2,
,解得ω=2,
∵g(x)=f(x![]() )=Acos[2(x
)=Acos[2(x![]() )+φ]=Acos(2x
)+φ]=Acos(2x![]() φ),且g(x)的圖象關于y軸對稱,
φ),且g(x)的圖象關于y軸對稱,
∴![]() φ=kπ,k∈Z,即φ=kπ
φ=kπ,k∈Z,即φ=kπ![]() ,k∈Z,
,k∈Z,
∴由|φ|![]() ,可得φ
,可得φ![]() ,可得f(x)=Acos(2x
,可得f(x)=Acos(2x![]() ),
),
∵![]() ,即f(
,即f(![]() )=Acos[2×(
)=Acos[2×(![]() )
)![]() ]=Acos0=A=2,
]=Acos0=A=2,
∴函數f(x)的解析式為![]() .
.
(2)由(1)知g(x)=2cos2x;
F(x)=2cos(2x![]() )+2cos2x=2(cos2xcos
)+2cos2x=2(cos2xcos![]() sin2xsin
sin2xsin![]() )+2cos2x=3cos2x
)+2cos2x=3cos2x![]() sin2x,
sin2x,
=2![]() cos(2x
cos(2x![]() );
);
∵x∈[0,aπ](a>0);
∴2x![]() ∈[
∈[![]() ,2aπ
,2aπ![]() ];
];
∵函數F(x)的圖象在x∈[0,aπ](a>0)上恰有2個最高點;
∴結合余弦函數的圖象(如圖示)知,4π≤2πa![]() 6π;
6π;
故解得a∈![]()
故實數a的取值范圍為![]() .
.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 是它的上頂點,點
是它的上頂點,點![]() 各不相同且均在橢圓上.
各不相同且均在橢圓上.
(1)若![]() 恰為橢圓長軸的兩個端點,求
恰為橢圓長軸的兩個端點,求![]() 的面積;
的面積;
(2)若![]() ,求證:直線
,求證:直線![]() 過一定點;
過一定點;
(3)若![]() ,
,![]() 的外接圓半徑為
的外接圓半徑為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:已知某公園的四處景觀分別位于等腰梯形![]() 的四個頂點處,其中
的四個頂點處,其中![]() ,
,![]() 兩地的距離為
兩地的距離為![]() 千米,
千米,![]() ,
,![]() 兩地的距離為
兩地的距離為![]() 千米,
千米,![]() .現擬規劃在
.現擬規劃在![]() (不包括端點)路段上增加一個景觀
(不包括端點)路段上增加一個景觀![]() ,并建造觀光路直接通往
,并建造觀光路直接通往![]() 處,造價為每千米
處,造價為每千米![]() 萬元,又重新裝飾
萬元,又重新裝飾![]() 路段,造價為每千米
路段,造價為每千米![]() 萬元.
萬元.
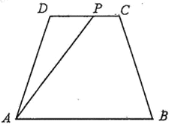
(1)若擬修建觀光路![]() 路段長為
路段長為![]() 千米,求
千米,求![]() 路段的造價;
路段的造價;
(2)設![]() ,當
,當![]() 為何值時,
為何值時,![]() ,
,![]() 段的總造價最低.
段的總造價最低.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,則
,則![]() ,
,![]() 為異面直線; ②若
為異面直線; ②若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
③若![]() ,
,![]() ,則
,則![]() ; ④若
; ④若![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
則上述命題中真命題的序號為( )
A.①②B.③④C.②D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 經過橢圓
經過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() ,且與橢圓
,且與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() 三點共線,直線
三點共線,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() (
(![]() ).
).
(1)求橢圓![]() 的方程;
的方程;
(2)當三角形![]() 的面積取得最大值時,求直線
的面積取得最大值時,求直線![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,點
上任意一點,點![]() 關于原點
關于原點![]() 的對稱點為點
的對稱點為點![]() ,有
,有![]() ,且當
,且當![]() 的面積最大時為等邊三角形.
的面積最大時為等邊三角形.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)與圓![]() 相切的直線
相切的直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,若橢圓上存在點
兩點,若橢圓上存在點![]() 滿足
滿足![]() ,求四邊形
,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com