
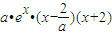 .((3分))
.((3分))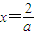 或x=-2.
或x=-2.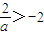 .
.
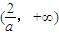 上單調遞增;在
上單調遞增;在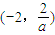 上單調遞減;(9分)
上單調遞減;(9分)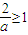 ,即0<a≤2時,函數f(t)在[0,1]上為減函數.ymin=f(1)=(a-4)e,ymax=f(0)=-2.
,即0<a≤2時,函數f(t)在[0,1]上為減函數.ymin=f(1)=(a-4)e,ymax=f(0)=-2. ,即a>2時,函數f(x)的極小值為[0,1]上的最小值,
,即a>2時,函數f(x)的極小值為[0,1]上的最小值,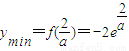 .
. 時,f(1)>f(0),此時ymax=f(1)=(a-4)e;
時,f(1)>f(0),此時ymax=f(1)=(a-4)e;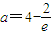 時,f(1)=f(0),此時ymax=f(0)=f(1)=-2;
時,f(1)=f(0),此時ymax=f(0)=f(1)=-2;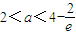 時,f(1)<f(0),此時ymax=f(0)=-2.(12分)
時,f(1)<f(0),此時ymax=f(0)=-2.(12分)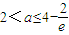 時,f(|cosx|)的最小值為
時,f(|cosx|)的最小值為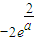 ,最大值為-2;
,最大值為-2;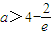 時,f(|cosx|)的最小值為
時,f(|cosx|)的最小值為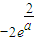 ,最大值為(a-4)e.(13分)
,最大值為(a-4)e.(13分)

 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com