
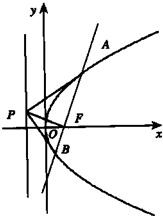
 如圖,設拋物線y2=2px(p>0)的焦點為F,經過點F的直線交拋物線于A、B兩點,且A、B兩點坐標為(x1,y1),(x2,y2),y1>0,y2<0,P是此拋物線的準線上的一點,O是坐標原點.
如圖,設拋物線y2=2px(p>0)的焦點為F,經過點F的直線交拋物線于A、B兩點,且A、B兩點坐標為(x1,y1),(x2,y2),y1>0,y2<0,P是此拋物線的準線上的一點,O是坐標原點.| PA |
| PB |
| p |
| 2 |
| p |
| 2 |
|
| p |
| 2 |
| p |
| 2 |
| y1-t | ||
x1+
|
| -t |
| p |
| y2-t | ||
x2+
|
| ||
| 2p |
| ||
| 2p |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
|
| p |
| 2 |
| p |
| 2 |
| y1-t | ||
x1+
|
| -t |
| p |
| y2-t | ||
x2+
|
| ||
| 2p |
| ||
| 2p |
| y1-t | ||
x1+
|
| y2-t | ||
x2+
|
| y1-t | ||||||
|
| y2-t | ||||||
|
| 2p(y1-t) | ||
|
| 2p(y2-t) | ||
|
(y1-t)(
| ||||
(
|
y1
| ||||||||
|
-t(
| ||||
p2(
|
| 2t |
| p |
| PA |
| PB |
| a-b |
| 1+ab |
| a-b |
| -ac+ab |
| a-b |
| a(b-c) |
| 1 |
| a |
| tanα-tanβ |
| 1+tanα•tanβ |
| -c-a |
| 1+(-c)a |
| a+c |
| 2 |


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
 如圖,設拋物線C1:y2=4mx(m>0)的準線與x軸交于F1,焦點為F2;以F1,F2為焦點,離心率e=
如圖,設拋物線C1:y2=4mx(m>0)的準線與x軸交于F1,焦點為F2;以F1,F2為焦點,離心率e=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:北京市海淀區2007年高三年級第一學期期末練習 數學(文科) 題型:044
| |||||||||||||||
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)當k=![]() 時,求雙曲線漸近線的斜率;
時,求雙曲線漸近線的斜率;
(Ⅱ)設拋物線的頂點為M,拋物線與直線y=kx的另一交點為C,是否存在實數k,使得△ACM的面積等于直線MA、MC的斜率的乘積的絕對值?若存在,求出k值;若不存在,說明理由.

查看答案和解析>>
科目:高中數學 來源:2006-2007學年重慶市南開中學高三(下)3月月考數學試卷(文科)(解析版) 題型:解答題
 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com