
(本小題滿分15分)已知函數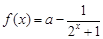 ,
,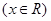 .
.
(1)用定義證明:不論 為何實數
為何實數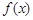 在
在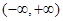 上為增函數;
上為增函數;
(2)若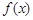 為奇函數,求
為奇函數,求 的值;
的值;
(3)在(2)的條件下,求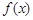 在區間[1,5]上的最小值.
在區間[1,5]上的最小值.
(1)見解析;(2)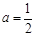 ;(3)
;(3) .
.
解析試題分析:(1)  的定義域為R, 任取
的定義域為R, 任取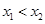 ,------------1分
,------------1分
則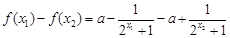 =
=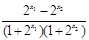 . -----------3分
. -----------3分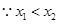 ,∴
,∴ 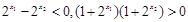 .
.
∴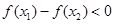 ,即
,即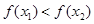 .
.
所以不論 為何實數
為何實數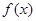 總為增函數.————————5分
總為增函數.————————5分
(2)  在
在 上為奇函數,
上為奇函數,
∴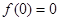 , ------------7分
, ------------7分
即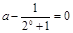 .解得
.解得 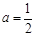 . —————————————10分
. —————————————10分
(3)由(2)知,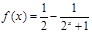 ,
,
由(1) 知,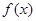 為增函數,
為增函數,
∴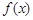 在區間
在區間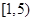 上的最小值為
上的最小值為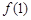 . ------------13分
. ------------13分
∵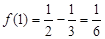 ,
,
∴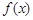 在區間
在區間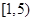 上的最小值為
上的最小值為 .———————————————15分
.———————————————15分
考點:本題考查用定義法證明函數的單調性;函數的奇偶性;函數的最值。
點評:(1)用的定義法證明函數單調性的步驟:一設二作差三變形四判斷符號五得出結論。
(2)靈活應用奇函數的性質:若x=0在函數的定義域內,則f(0)=0。屬于基礎試題。


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:解答題
(本題滿分12分)
把邊長為 的等邊三角形鐵皮剪去三個相同的四邊形(如圖陰影部分)后,用剩余部分做成一個無蓋的正三棱柱形容器(不計接縫),設容器的高為
的等邊三角形鐵皮剪去三個相同的四邊形(如圖陰影部分)后,用剩余部分做成一個無蓋的正三棱柱形容器(不計接縫),設容器的高為 ,容積為
,容積為 .
.
(Ⅰ)寫出函數 的解析式,并求出函數的定義域;
的解析式,并求出函數的定義域;
(Ⅱ)求當x為多少時,容器的容積最大?并求出最大容積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)星期天,劉先生到電信局打算上網開戶,經詢問,記錄了可能需要的三種方式所花費的費用資料,現將資料整理如下:
1163普通:上網資費2元/小時;
2163A:每月50元(可上網50小時),超過50小時的部分資費2元/小時;
3ADSLD:每月70元,時長不限(其他因素忽略不計).
請你用所學的函數知識對上網方式與費用問題作出研究:
(1)分別寫出三種上網方式中所用資費與時間的函數解析式;
(2)在同一坐標系內分別畫出三種方式所需資費與時間的函數圖象;
(3)根據你的研究,請給劉先生一個合理化的建議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com