
分析 由題意可知:設AB=BC=1,假設AB在x軸上,設橢圓方程為:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),由余弦定理可知:丨AC丨2=3,則丨AC丨=$\sqrt{3}$,2a=$\sqrt{3}$+1,a=$\frac{\sqrt{3}+1}{2}$,2c=1,c=$\frac{1}{2}$,e=$\frac{c}{a}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}+1}{2}}$=$\frac{{\sqrt{3}-1}}{2}$,即可求得橢圓的離心率.
解答  解:設AB=BC=1,假設AB在x軸上,設橢圓方程為:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
解:設AB=BC=1,假設AB在x軸上,設橢圓方程為:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由余弦定理可知:丨AC丨2=丨AB丨2+丨BC丨2-2丨AB丨•丨BC丨•cosB=1+1-2×1×1×(-$\frac{1}{2}$)=3
∴丨AC丨=$\sqrt{3}$,
∵以A、B為焦點的橢圓經過點C,
∴2a=$\sqrt{3}$+1,a=$\frac{\sqrt{3}+1}{2}$,2c=1,c=$\frac{1}{2}$,
∴e=$\frac{c}{a}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}+1}{2}}$=$\frac{{\sqrt{3}-1}}{2}$,
故答案為:$\frac{{\sqrt{3}-1}}{2}$.
點評 本題考查余弦定理的運用,考查橢圓的幾何性質及標準方程的應用,屬于基礎題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
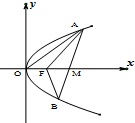 已知拋物線C:y2=2px(p>0),焦點F($\frac{p}{2}$,0),如果存在過點M(x0,0)$({x_0}>\frac{p}{2})$的直線l與拋物線C交于不同的兩點A、B,使得S△AOM=λ•S△FAB,則稱點M為拋物線C的“λ分點”.
已知拋物線C:y2=2px(p>0),焦點F($\frac{p}{2}$,0),如果存在過點M(x0,0)$({x_0}>\frac{p}{2})$的直線l與拋物線C交于不同的兩點A、B,使得S△AOM=λ•S△FAB,則稱點M為拋物線C的“λ分點”.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x2+(y-1)2=3 | B. | x2+(y-1)2=4 | C. | x2+(y-1)2=12 | D. | x2+(y-1)2=16 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x | -2 | 0 | 1 | 3 | 8 |
| f′(x) | -10 | 6 | 8 | 0 | -90 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
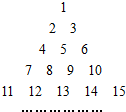 將全體正整數排成一個三角形數陣:按照如圖所示排列的規律:
將全體正整數排成一個三角形數陣:按照如圖所示排列的規律:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com