
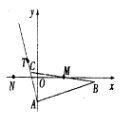
【題目】如圖,已知![]() 的邊
的邊![]() 所在直線的方程為
所在直線的方程為![]() ,
,![]() 滿足
滿足![]() ,點
,點![]() 在
在![]() 邊所在直線上且滿足
邊所在直線上且滿足![]() .
.
(1)求![]() 邊所在直線的方程;
邊所在直線的方程;
(2)求![]() 外接圓的方程;
外接圓的方程;
(3)若動圓![]() 過點
過點![]() ,且與
,且與![]() 的外接圓外切,求動圓
的外接圓外切,求動圓![]() 的圓心的軌跡方程.
的圓心的軌跡方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)由已知![]() 可得
可得![]() 為
為![]() ,由
,由![]() 邊所在直線的方程為
邊所在直線的方程為![]() ,可求直線
,可求直線![]() 的斜率,點
的斜率,點![]() 在直線
在直線![]() 上,利用直線的點斜式可求;(2)
上,利用直線的點斜式可求;(2)![]() 與
與![]() 的交點
的交點![]() ,聯立方程可求
,聯立方程可求![]() 的坐標,由
的坐標,由![]() 結合直角三角形的性質可得
結合直角三角形的性質可得![]() 的外接圓的圓心,進而可求
的外接圓的圓心,進而可求![]() ,外接圓的方程可求;(3)由題意可得
,外接圓的方程可求;(3)由題意可得![]() ,即
,即![]() ,結合圓錐曲線的定義可求軌跡方程.
,結合圓錐曲線的定義可求軌跡方程.
試題解析:(1)![]() ,又
,又![]() 在
在![]() 上,
上,
![]() ,
,![]() 為
為![]() ,
,
又![]() 邊所在直線的方程為
邊所在直線的方程為![]() ,所以直線
,所以直線![]() 的斜率為
的斜率為![]() ,又因為點
,又因為點![]()
在直線![]() 上,所以
上,所以![]() 邊所在直線的方程為:
邊所在直線的方程為:![]() ,即
,即![]() .
.
(2)![]() 與
與![]() 的交點為
的交點為![]() ,所以由
,所以由![]()
解得點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,![]() 為
為![]() 斜邊上的中點,即為
斜邊上的中點,即為![]() 外接圓的圓心,又
外接圓的圓心,又![]() ,
,
從而![]() 外接圓的方程為:
外接圓的方程為:![]() .
.
(3)因為動圓![]() 過點
過點![]() ,所以
,所以![]() 是該圓的半徑,又因為動圓
是該圓的半徑,又因為動圓![]() 與圓
與圓![]() 外切,
外切,
所以![]() ,即
,即![]() .
.
故點![]() 的軌跡是以
的軌跡是以![]() ,
,![]() 為焦點,實軸長為
為焦點,實軸長為![]() 的雙曲線的左支.
的雙曲線的左支.
因為實半軸長![]() ,半焦距
,半焦距![]() .
.
所以虛半軸長![]() .
.
從而動圓![]() 的圓心的軌跡方程為
的圓心的軌跡方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】某企業生產A,B兩種產品,根據市場調查與市場預測,知A產品的利潤與投資成正比,其關系如圖1,B產品的利潤與投資的算術平方根成正比,其關系如圖2.(注:所示圖中的橫坐標表示投資金額,單位:萬元)

圖1 圖2
(1)分別將A,B兩種產品的利潤表示為投資的函數關系式;
(2)該企業已籌集10萬元資金,并全部投入A,B兩種產品的生產,問:怎樣分配這10萬元資金,才能使企業獲得最大利潤,最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 是過點
是過點![]() ,傾斜角為
,傾斜角為![]() 的直線,以直角坐標系
的直線,以直角坐標系![]() 的原點為極點,
的原點為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的一個參數方程;
的一個參數方程;
(2)曲線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家分析發現“喜歡空間想象”與“性別”有關,某數學興趣小組為了驗證此結論,從全體組員中按分層抽樣的方法抽取50名同學(男生30人、女生20人),給每位同學立體幾何題、代數題各一道,讓各位同學自由選擇一道題進行解答,選題情況統計如下表:(單位:人)
立體幾何題 | 代數題 | 總計 | |
男同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握認為“喜歡空間想象”與“性別”有關?
(2)經統計得,選擇做立體幾何題的學生正答率為![]() ,且答對的學生中男生人數是女生人數的5倍,現從選擇做立體幾何題且答錯的學生中任意抽取兩人對他們的答題情況進行研究,求恰好抽到男女生各一人的概率.
,且答對的學生中男生人數是女生人數的5倍,現從選擇做立體幾何題且答錯的學生中任意抽取兩人對他們的答題情況進行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地政府決定建造一批保障房供給社會,緩解貧困人口的住房問題,計劃用1 600萬元購得一塊土地,在該土地上建造10幢樓房的住宅小區,每幢樓的樓層數相同,且每層建筑面積均為1 000平方米,每平方米的建筑費用與樓層有關,第x層樓房每平方米的建筑費用為(kx+800)元(其中k為常數).經測算,若每幢樓為5層,則該小區每平方米的平均綜合費用為1 270元.
注:每平方米平均綜合費用=![]() .
.
(1) 求k的值;
(2) 問要使該小區樓房每平方米的平均綜合費用最低,應將這10幢樓房建成多少層?此時每平方米的平均綜合費用為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥研究所開發的一種藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升中的含藥量![]() (微克)與時間
(微克)與時間![]() (小時)之間近似滿足如圖所示的曲線.(當
(小時)之間近似滿足如圖所示的曲線.(當![]() 時,
時, ![]() ).
).
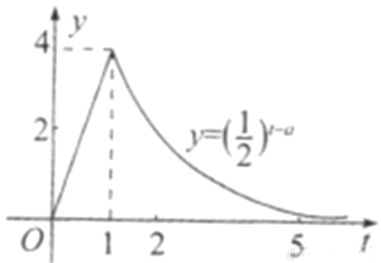
(1)寫出第一次服藥后![]() 與
與![]() 之間的函數關系式
之間的函數關系式![]() ;
;
(2)據進一步測定,每毫升血液中含藥量不少于![]() 微克時,治療疾病有效,求服藥一次后治療疾病有效時間.
微克時,治療疾病有效,求服藥一次后治療疾病有效時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上的動點
上的動點![]() 滿足到點
滿足到點![]() 的距離比到直線
的距離比到直線![]() 的距離小1.
的距離小1.
(1)求曲線![]() 的方程;
的方程;
(2)動點![]() 在直線
在直線![]() 上,過點
上,過點![]() 分別作曲線
分別作曲線![]() 的切線
的切線![]() ,切點為
,切點為![]() .直線
.直線![]() 是否恒過定點,若是,求出定點坐標,若不是,請說明理由.
是否恒過定點,若是,求出定點坐標,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com