
【題目】下列關于函數![]() 的敘述正確的為( )
的敘述正確的為( )
A.函數![]() 有三個零點
有三個零點
B.點(1,0)是函數![]() 圖象的對稱中心
圖象的對稱中心
C.函數![]() 的極大值點為
的極大值點為![]()
D.存在實數a,使得函數![]() 為增函數
為增函數
【答案】ABC
【解析】
令函數等于零即可求出零點個數,可判斷出選項A;由![]() 可得出函數圖像關于點(1,0)中心對稱,可判斷出選項B;由導函數求出函數單調區間,根據函數單調性即可得出最大值點,可判斷出選項C;根據導函數判斷出是否存在實數a,使得
可得出函數圖像關于點(1,0)中心對稱,可判斷出選項B;由導函數求出函數單調區間,根據函數單調性即可得出最大值點,可判斷出選項C;根據導函數判斷出是否存在實數a,使得![]() ,可判斷出選項D.
,可判斷出選項D.
![]() ,令
,令![]() ,則
,則![]() 或
或![]() 或
或![]() ,
,
所以函數![]() 有三個零點,所以A正確;
有三個零點,所以A正確;
![]() ,
,
![]() ,
,
所以![]() ,所以函數
,所以函數![]() 圖像關于點(1,0)對稱中心,
圖像關于點(1,0)對稱中心,
所以B正確;求出![]() 的導函數
的導函數![]() ,
,
令![]() ,則
,則![]() 或
或![]() ,
,
令![]() ,則
,則![]() ,
,
所以函數![]() 在
在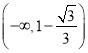 和
和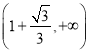 上單調遞增,
上單調遞增,
在 上單調遞減,所以當
上單調遞減,所以當![]() 時
時
函數![]() 有極大值,所以函數
有極大值,所以函數![]() 的極大值點為
的極大值點為![]() ,
,
所以C正確;假設函數![]() 為增函數,
為增函數,
則![]() 恒成立,由上可知當
恒成立,由上可知當![]() 或
或![]() 時,
時,
![]() ,若要滿足
,若要滿足![]() ,則需在
,則需在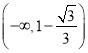 和
和
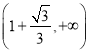 上
上![]() 恒成立,
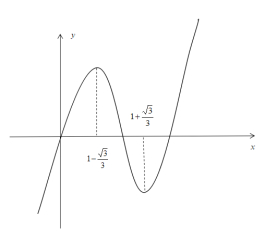
恒成立,![]() 圖像如下,
圖像如下,
如圖所示函數![]() 在
在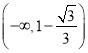 上不可能恒成立,所以不存在這樣的實數a,所以D錯誤.
上不可能恒成立,所以不存在這樣的實數a,所以D錯誤.
故選:ABC


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】某高校設計了一個實驗學科的實驗考查方案:考生從6道備選題中一次性隨機抽取3題,按照題目要求獨立完成全部實驗操作.規定:至少正確完成其中2題的便可提交通過.已知6道備選題中考生甲有4道題能正確完成,2道題不能完成.
(1)求出甲考生正確完成題數的概率分布列,并計算數學期望;
(2)若考生乙每題正確完成的概率都是![]() ,且每題正確完成與否互不影響.試從至少正確完成2題的概率分析比較兩位考生的實驗操作能力.
,且每題正確完成與否互不影響.試從至少正確完成2題的概率分析比較兩位考生的實驗操作能力.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,且滿足_______.
,且滿足_______.
(Ⅰ)求函數![]() 的解析式及最小正周期;
的解析式及最小正周期;
(Ⅱ)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不同解,求實數
上有兩個不同解,求實數![]() 的取值范圍.從①
的取值范圍.從①![]() 的最大值為
的最大值為![]() ,②
,②![]() 的圖象與直線
的圖象與直線![]() 的兩個相鄰交點的距離等于
的兩個相鄰交點的距離等于![]() ,③
,③![]() 的圖象過點
的圖象過點![]() .這三個條件中選擇一個,補充在上面問題中并作答.
.這三個條件中選擇一個,補充在上面問題中并作答.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①acosB+bcosA=![]() cosC;②2asinAcosB+bsin2A=
cosC;②2asinAcosB+bsin2A=![]() a;③△ABC的面積為S,且4S=
a;③△ABC的面積為S,且4S=![]() (a2+b2-c2),這三個條件中任意選擇一個,填入下面的問題中,并求解,在銳角△ABC中,角A,B,C所對的邊分別為a,b,c,函數
(a2+b2-c2),這三個條件中任意選擇一個,填入下面的問題中,并求解,在銳角△ABC中,角A,B,C所對的邊分別為a,b,c,函數![]() =2
=2![]() sinωxcosωx+2cos2ωx的最小正周期為π,c為
sinωxcosωx+2cos2ωx的最小正周期為π,c為![]() 在[0,
在[0,![]() ]上的最大值,求a-b的取值范圍.注:如果選擇多個條件分別解答,那么按第一個解答計分.
]上的最大值,求a-b的取值范圍.注:如果選擇多個條件分別解答,那么按第一個解答計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() ,橢圓上一點到左焦點的距離的取值范圍為
,橢圓上一點到左焦點的距離的取值范圍為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() ,
,![]() ,
,![]() ,
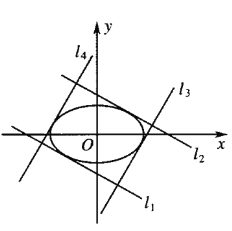
,![]() 分別與橢圓相切,且
分別與橢圓相切,且![]() ,
,![]() ,
,![]() ,如圖,
,如圖,![]() ,
,![]() ,
,![]() ,
,![]() 圍成的矩形的面積記為
圍成的矩形的面積記為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四邊形ABCD中,BD為四邊形的一條對角線,且![]() ,將
,將![]() 沿BD向上翻折,當點A在平面BCD內的投影恰好為
沿BD向上翻折,當點A在平面BCD內的投影恰好為![]() 的外心E時,設直線AE與平面ABC,ACD,ABD的夾角分別為
的外心E時,設直線AE與平面ABC,ACD,ABD的夾角分別為![]() ,
,![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com