
【題目】設函數f(x)= ![]() (其中p2+q2≠0),且存在公差不為0的無窮等差數列{an},使得函數在其定義域內還可以表示為f(x)=1+a1x+a2x+a2x2+…+anxn+…
(其中p2+q2≠0),且存在公差不為0的無窮等差數列{an},使得函數在其定義域內還可以表示為f(x)=1+a1x+a2x+a2x2+…+anxn+…
(1)求a1 , a2的值(用p,q表示);
(2)求{an}的通項公式;
(3)當n∈N*且n≥2時,比較(an﹣1)an與(an) ![]() 的大小.
的大小.
【答案】
(1)解:由題意,得 ![]() ,
,
顯然x,x2的系數為0,所以 ![]() ,
,
從而a1=﹣p, ![]()
(2)解:考慮xn(n≥3)的系數,則有an+pan﹣1+qan﹣2=0,
因數列{an}是等差數列,所以an﹣2an﹣1+an﹣2=0,所以(2+p)an﹣1=(1﹣q)an﹣2對一切n≥3都成立,
若an=0,則p=q=0,與p2+q2≠0矛盾,
若數列{an}是等比數列,又據題意{an}是等差數列,則{an}是常數列,這與數列{an}的公差不為零矛盾,
所以2+p=1﹣q=0,即p=﹣2,q=1,
由(1)知a1=2,a2=3,所以an=n+1.
(其他方法:根據題意可以用p、q表示出a1,a2,a3,a4,由數列{an}為等差數列,利用2a2=a1+a3,2a3=a2+a4解方程組也可求得.其它解法酌情給分.)
(3)解:由(2)可得:(an﹣1)an=nn+1,(an) ![]() =(n+1)n
=(n+1)n
當n=2時,a1a2=23,=8,a2a1=32,=9,∴a1a2<a2a1.
當n≥3時,nn+1>(n+1)n即(an﹣1)an>(an) ![]() ,下面用數學歸納法證明.
,下面用數學歸納法證明.
①當n=3時,34=81,43=64,∴64<81.結論成立.
②假設n=k時,結論成立,即kk+1>(k+1)k.
下面證明n=k+1時成立.
由假設得 ![]() ,因為(k+1)2>k(k+2),即:
,因為(k+1)2>k(k+2),即: ![]() ,
,
所以 ![]() >
> ![]() =
= ![]() ,
,
即(k+1)k+2>(k+2)k+1.所以n=k+1時,結論也成立.
綜上n∈N*且n≥3時,(an﹣1)an>(an) ![]()
【解析】(1)化簡已知條件,利用方程的系數關系列出方程,求解即可.(2)考慮xn(n≥3)的系數,推出an+pan﹣1+qan﹣2=0,利用數列{an}是等差數列,數列{an}是等比數列,推出矛盾,利用(1)知a1=2,a2=3,求出an . (3)通過當n=2時,推出a1a2<a2a1 . 當n≥3時,(an﹣1)an>(an) ![]() ,利用數學歸納法證明即可.
,利用數學歸納法證明即可.
【考點精析】利用等差數列的性質對題目進行判斷即可得到答案,需要熟知在等差數列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數列是等差數列.


 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案科目:高中數學 來源: 題型:
【題目】已知圓![]() ,某拋物線的頂點為原點
,某拋物線的頂點為原點![]() ,焦點為圓心
,焦點為圓心![]() ,經過點
,經過點![]() 的直線
的直線![]() 交圓
交圓![]() 于
于![]() ,
, ![]() 兩點,交此拋物線于
兩點,交此拋物線于![]() ,
, ![]() 兩點,其中
兩點,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求該拋物線的方程;
(2)是否存在直線![]() ,使
,使![]() 是
是![]() 與
與![]() 的等差中項?若存在,求直線
的等差中項?若存在,求直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數z=(a2﹣7a+6)+(a2﹣5a﹣6)i(a∈R)
(1)若復數z為純虛數,求實數a的值;
(2)若復數z在復平面內的對應點在第四象限,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
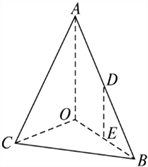
【題目】如圖,在三棱錐![]() 中,
中, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.(19)
的中點.(19)
(I)求![]() 到平面
到平面![]() 的距離;
的距離;
(II)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() ∥平面
∥平面![]() ,若存在,試確定
,若存在,試確定![]() 的位置,并證明此點滿足要求;若不存在,請說明理由.
的位置,并證明此點滿足要求;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,{bn}是等比數列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通項公式;
(Ⅱ)設cn=an+bn , 求數列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,{bn}是等比數列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通項公式;
(Ⅱ)設cn=an+bn , 求數列{cn}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com