
【題目】如圖,過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() 分別作直線
分別作直線![]() ,
, ![]() 交橢圓于
交橢圓于![]() 與
與![]() ,且
,且![]() .
.
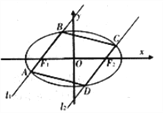
(1)求證:當直線![]() 的斜率
的斜率![]() 與直線
與直線![]() 的斜率
的斜率![]() 都存在時,
都存在時, ![]() 為定值;
為定值;
(2)求四邊形![]() 面積的最大值.
面積的最大值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析: (1)設![]() ,分別將
,分別將![]() 坐標代入橢圓中,得出兩等式,相減得出
坐標代入橢圓中,得出兩等式,相減得出![]() ,寫出
,寫出![]() 的表達式,化簡得出結果; (2)設直線
的表達式,化簡得出結果; (2)設直線![]() 的方程
的方程![]() ,聯立直線
,聯立直線![]() 的方程和橢圓方程,求出
的方程和橢圓方程,求出![]() ,算出
,算出![]() 的表達式,而
的表達式,而![]() ,代入,用基本不等式求出最大值,再得出四邊形
,代入,用基本不等式求出最大值,再得出四邊形![]() 面積的最大值.
面積的最大值.
試題解析: (1)設![]() ,
, ![]() ,根據對稱性,有
,根據對稱性,有![]() ,因為
,因為![]() ,
, ![]() 都在橢圓
都在橢圓![]() 上,所以
上,所以![]() ,
, ![]() ,二式相減得,
,二式相減得, ![]() ,所以
,所以![]() 為定值.
為定值.
(2)當![]() 的傾斜角為
的傾斜角為![]() 時,
時, ![]() 與
與![]() 重合,舍去.
重合,舍去.
當![]() 的傾斜角不為0時,由對稱性得四邊形
的傾斜角不為0時,由對稱性得四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,代入
,代入![]() ,得
,得![]() .顯然
.顯然![]() ,
, ![]() ,
, ![]() .
.
所以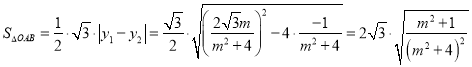
設![]() ,所以
,所以![]() ,
, ![]() .所以
.所以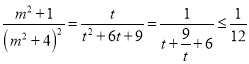 .
.
當且僅當![]() 即
即![]() 時等號成立,所以
時等號成立,所以![]() .
.
所以平行四邊形面積的最大值為![]() .
.
點睛: 本題主要考查直線與橢圓相交時的有關知識,考查學生分析問題解決問題的能力,屬于中檔題.解題技巧: 在(1)中,采用設而不求;在(2)中, 設直線![]() 的方程
的方程![]() 比
比![]() 好,因為聯立直線與橢圓方程計算量減少,還有
好,因為聯立直線與橢圓方程計算量減少,還有![]() ,由韋達定理可求出
,由韋達定理可求出![]() .在求三角形
.在求三角形![]() 面積最大值時,將
面積最大值時,將![]() 看成一個整體,利用基本不等式求出最大值.
看成一個整體,利用基本不等式求出最大值.


科目:高中數學 來源: 題型:
【題目】下列命題:
·(1)y=|cos(2x+ ![]() )|最小正周期為π;
)|最小正周期為π;
·(2)函數y=tan ![]() 的圖象的對稱中心是(kπ,0),k∈Z;
的圖象的對稱中心是(kπ,0),k∈Z;
·(3)f(x)=tanx﹣sinx在(﹣ ![]() ,
, ![]() )上有3個零點;
)上有3個零點;
·(4)若 ![]() ∥
∥ ![]() ,
, ![]() ,則
,則 ![]()
其中錯誤的是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校計劃面向高一年級![]() 名學生開設校本選修課程,為確保工作的順利實施,先按性別進行分層抽樣,抽取了
名學生開設校本選修課程,為確保工作的順利實施,先按性別進行分層抽樣,抽取了![]() 名學生對社會科學類,自然科學類這兩大類校本選修課程進行選課意向調查,其中男生有
名學生對社會科學類,自然科學類這兩大類校本選修課程進行選課意向調查,其中男生有![]() 人.在這
人.在這![]() 名學生中選擇社會科學類的男生、女生均為
名學生中選擇社會科學類的男生、女生均為![]() 人.
人.
(Ⅰ)分別計算抽取的樣本中男生及女生選擇社會科學類的頻率,并以統計的頻率作為概率,估計實際選課中選擇社會科學類學生數;
(Ⅱ)根據抽取的![]() 名學生的調查結果,完成下列列聯表.并判斷能否在犯錯誤的概率不超過
名學生的調查結果,完成下列列聯表.并判斷能否在犯錯誤的概率不超過![]() 的前提下認為科類的選擇與性別有關?
的前提下認為科類的選擇與性別有關?
選擇自然科學類 | 選擇社會科學類 | 合計 | |
男生 | |||
女生 | |||
合計 |
附: 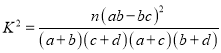 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
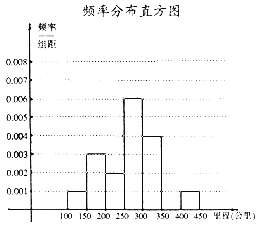
【題目】面對全球范圍內日益嚴峻的能源形勢與環保壓力,環保與低碳成為今后汽車發展的一大趨勢,越來越多的消費者對新能源汽車表示出更多的關注,某研究機構從汽車市場上隨機抽取N輛純電動汽車調查其續航里程(單次充電后能行駛的最大里程),被調查汽車的續航里程全部介于100公里和450公里之間,根據調查數據形成了如圖所示頻率分布表及頻率分布直方圖.
頻率分布表
分組 | 頻數 | 頻率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合計 | N | 1 |
(1)試確定頻率分布表中x,y,N的值,并補全頻率分布直方圖;
(2)若從續航里程在[200,250)及[350,400)的車輛中隨機抽取2輛車,求兩輛車續航里程都在[350,400)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+![]() x2+mx在x=1處有極小值,
x2+mx在x=1處有極小值,
g(x)=f(x)﹣![]() x3﹣
x3﹣![]() x2+x﹣alnx.
x2+x﹣alnx.
(1)求函數f(x)的單調區間;
(2)是否存在實數a,對任意的x1、x2∈(0,+∞),且x1≠x2,有![]() 恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知橢圓的左焦點為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() (
(![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
(ⅰ)若點![]() 的橫坐標為1,求
的橫坐標為1,求![]() 的面積;
的面積;
(ⅱ)直線![]() 是否恒過定點?若過定點,求出該定點的坐標;若不過定點,請說明理由.
是否恒過定點?若過定點,求出該定點的坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
已知直線l經過點![]() ,傾斜角
,傾斜角![]() ,圓
,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出直線l的參數方程,并把圓![]() 的方程化為直角坐標方程;
的方程化為直角坐標方程;
(Ⅱ)設l與圓![]() 相交于
相交于![]() 兩點,求點
兩點,求點![]() 到
到![]() 兩點的距離之積.
兩點的距離之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:若函數y=f(x)在某一區間D上任取兩個實數x1、x2 , 且x1≠x2 , 都有 ![]() ,則稱函數y=f(x)在區間D上具有性質L.
,則稱函數y=f(x)在區間D上具有性質L.
(1)寫出一個在其定義域上具有性質L的對數函數(不要求證明).
(2)對于函數 ![]() ,判斷其在區間(0,+∞)上是否具有性質L?并用所給定義證明你的結論.
,判斷其在區間(0,+∞)上是否具有性質L?并用所給定義證明你的結論.
(3)若函數 ![]() 在區間(0,1)上具有性質L,求實數a的取值范圍.
在區間(0,1)上具有性質L,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com