
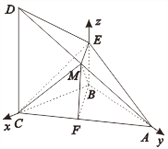
【題目】已知四棱錐A-BCDE中,底面BCDE為直角梯形,CD⊥平面ABC,側面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,點M是棱AD的中點

(I)證明:平面AED⊥平面ACD;
(Ⅱ)求銳二面角B-CM-A的余弦值
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:(1)![]() 平面ACD,又EM//BF,所以
平面ACD,又EM//BF,所以![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;(2)建立空間直角坐標系,求得兩個法向量
;(2)建立空間直角坐標系,求得兩個法向量![]() ,
,![]() ,求出二面角。
,求出二面角。
試題解析:
(I)證明:取AC的中點F,連接BF,
因為AB=BC,所以![]() ,
, ![]() 平面ABC,所以CD
平面ABC,所以CD ![]() .
.
又![]() 所以
所以![]() 平面ACD.①
平面ACD.①
因為AM=MD,AF=CF,所以![]() .
.
因為![]()
![]() ,所以
,所以![]() //MF,
//MF,
所以四邊形BFME是平行四邊形.所以EM//BF.②
由①②,得![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;
;
(II)![]() BE
BE![]() 平面ABC,
平面ABC,
![]() 又
又![]() ,
,
![]() 以點B為原點,直線BC、BA、BE分別為x,y,z軸,
以點B為原點,直線BC、BA、BE分別為x,y,z軸,
建立空間直角坐標系B-xyz.
由![]() ,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
由中點坐標公式得![]() ,
, ![]() ,
,![]() ,
,
設向量![]() 為平面BMC的一個法向量,則
為平面BMC的一個法向量,則![]() 即
即![]()
令y=1,得x=0,z=-1,即![]() ,
,
由(I)知, ![]() 是平面ACD的一個法向量.
是平面ACD的一個法向量.
設二面角B-CM-A的平面角為![]() ,
,
則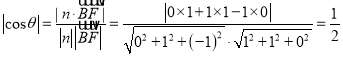 ,
,
又二面角B-CM-A為銳二面角,故![]() .
.


科目:高中數學 來源: 題型:
【題目】在棱長為1的正方體![]() 中,點
中,點![]() ,
, ![]() 分別是側面
分別是側面![]() 與底面
與底面![]() 的中心,則下列命題中錯誤的個數為( )
的中心,則下列命題中錯誤的個數為( )
①![]() 平面
平面![]() ; ②異面直線
; ②異面直線![]() 與
與![]() 所成角為
所成角為![]() ;
;
③![]() 與平面
與平面![]() 垂直; ④
垂直; ④![]() .
.
A. 0 B. 1 C. 2 D. 3
【答案】A
【解析】對于①,∵DF![]() ,DF
,DF![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,正確;
,正確;
對于②,∵DF![]() ,∴異面直線
,∴異面直線![]() 與
與![]() 所成角即異面直線
所成角即異面直線![]() 與
與![]() 所成角,△
所成角,△![]() 為等邊三角形,故異面直線
為等邊三角形,故異面直線![]() 與
與![]() 所成角為
所成角為![]() ,正確;
,正確;
對于③,∵![]() ⊥
⊥![]() ,
, ![]() ⊥CD,且
⊥CD,且![]() CD=D,∴
CD=D,∴![]() ⊥平面
⊥平面![]() ,即
,即![]() ⊥平面
⊥平面![]() 正確;
正確;
對于④,![]() ,正確,
,正確,
故選:A
【題型】單選題
【結束】
8
【題目】已知函數![]() 在區間
在區間![]() 上單調遞增,則實數
上單調遞增,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的長軸長是短軸長的2倍,
的長軸長是短軸長的2倍,![]() 是橢圓
是橢圓![]() 的右焦點,直線
的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點.當
兩點.當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為對南康區和于都縣兩區縣某次聯考成績進行分析,隨機抽查了兩地一共10000名考生的成績,根據所得數據畫了如下的樣本頻率分布直方圖.

(1)求成績在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據平均數;
(3)為了分析成績與班級、學校等方面的關系,必須按成績再從這10000人中用分層抽樣方法抽出20人作進一步分析,則成績在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓C與y軸相切于點T(0,2),與x軸的正半軸交于兩點![]() (點
(點![]() 在點
在點![]() 的左側),且
的左側),且![]() .
.
(1)求圓C的方程;(2)過點![]() 任作一直線與圓O:
任作一直線與圓O: ![]() 相交于
相交于![]() 兩點,連接
兩點,連接![]() ,求證:
,求證: ![]() 定值.
定值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為[﹣1,1],圖象如圖1所示;函數g(x)的定義域為[﹣2,2],圖象如圖2所示,設函數f(g(x))有m個零點,函數g(f(x))有n個零點,則m+n等于( )
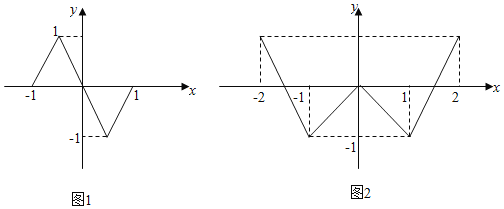
A. 6 B. 10 C. 8 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中, ![]() 的兩個頂點
的兩個頂點![]() 的坐標分別為
的坐標分別為![]() ,三個內角
,三個內角![]() 滿足
滿足![]() .
.
(1)若頂點![]() 的軌跡為
的軌跡為![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(2)若點![]() 為曲線
為曲線![]() 上的一點,過點
上的一點,過點![]() 作曲線
作曲線![]() 的切線交圓
的切線交圓![]() 于不同的兩點
于不同的兩點![]() (其中
(其中![]() 在
在![]() 的右側),求四邊形
的右側),求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com