【題目】已知函數
(其中e是自然對數的底數，k∈R)．
(1)討論函數
的單調性；
(2)當函數
有兩個零點
時，證明： 
．
【答案】（1）見解析；（2）見解析.
【解析】試題分析：
本題考查導數與函數單調性的關系以及用導數證明不等式的問題。（1）求導數后，根據導函數的符號判斷出函數的單調性。（2）根據題意將證明
的問題轉化為證明
，即證
，構造函數
，
利用函數
的單調性證明即可。
試題解析：
（1）解：∵
∴
。
①當
時，令
，解得
，
∴當
時，
，
單調遞減；
當
時，
，單調遞增。
②當
時，
恒成立，
∴函數在R上單調遞增.
綜上，當時，在
上單調遞減，在
上單調遞增。
當時，在R上單調遞增.
（2）證明：當
時，由（1）知函數單調遞增，不存在兩個零點。
所以
。
設函數的兩個零點為
，
則
，
設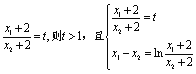
，
解得
，
所以
，
要證
，
只需證
，
設
設
單調遞增，
所以
，
所以
在區間
上單調遞增，
所以
，
故
．
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，C1的參數方程為
(t為參數)，在以坐標原點為極點，x軸正半軸為極軸的極坐標系中，C2的極坐標方程ρ2－2ρcos θ－3＝0.
(Ⅰ)說明C2是哪種曲線，并將C2的方程化為普通方程；
(Ⅱ)C1與C2有兩個公共點A，B，定點P的極坐標
，求線段AB的長及定點P到A，B兩點的距離之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
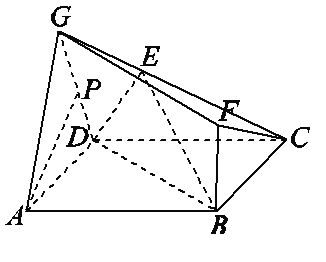
【題目】如圖所示的多面體中，底面ABCD為正方形，△GAD為等邊三角形，BF⊥平面ABCD，∠GDC＝90°，點E是線段GC上除兩端點外的一點，若點P為線段GD的中點．
(Ⅰ)求證：AP⊥平面GCD；
(Ⅱ)求證：平面ADG∥平面FBC；
(Ⅲ)若AP∥平面BDE，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E： 
經過點
，離心率為
.
(1)求橢圓E的標準方程；
(2)若A1，A2分別是橢圓E的左、右頂點，過點A2作直線l與x軸垂直，點P是橢圓E上的任意一點(不同于橢圓E的四個頂點)，連接PA1交直線l于點B，點Q為線段A2B的中點，求證：直線PQ與橢圓E只有一個公共點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知拋物線x2＝y，點
，拋物線上的點
，過點B作直線AP的垂線，垂足為Q.
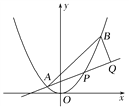
(1)求直線AP斜率的取值范圍；
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，PA⊥平面ABCD，AB⊥AD，，AC＝AD＝CD，E是AD的中點．
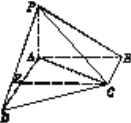
(Ⅰ)證明CE∥平面PAB；
(Ⅱ)證明：平面PAD⊥平面PCE.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC－A1B1C1中，CC1⊥平面ABC，M是CC1中點．
(Ⅰ)求證：平面AB1M⊥平面A1ABB1；
(Ⅱ)過點C作一截面與平面AB1M平行，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)，長軸長為4，離心率為
.
(Ⅰ)橢圓的求橢圓的標準方程；
(Ⅱ)設過定點M(0,2)的直線l與橢圓C交于不同的兩點A，B，且∠AOB為銳角(O為坐標原點)，求直線l的斜率k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校對2000名高一新生進行英語特長測試選拔，現抽取部分學生的英語成績，將所得數據整理后得出頻率分布直方圖如圖所示，圖中從左到右各小長方形面積之比為
，第二小組頻數為12．
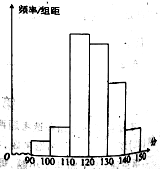
（Ⅰ）求第二小組的頻率及抽取的學生人數；
（Ⅱ）若分數在120分以上（含120分）才有資格被錄取，約有多少學生有資格被錄取？
（Ⅲ）學校打算從分數在
和
分內的學生中，按分層抽樣抽取4人進行改進意見問卷調查，若調查老師隨機從這4人的問卷中（每人一份）隨機抽取兩份調閱，求這兩份問卷都來自英語測試成績在分的學生的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com