
【題目】學校為測評班級學生對任課教師的滿意度,采用“100分制”打分的方式來計分.現從某班學生中隨機抽取10名,以下莖葉圖記錄了他們對某教師的滿意度分數(以十位數字為莖,個位數字為葉):
規定若滿意度不低于98分,測評價該教師為“優秀”.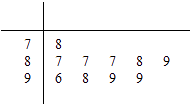
(1)求從這10人中隨機選取3人,至多有1人評價該教師是“優秀”的概率;
記ξ表示抽到評價該教師為“優秀”的人數,求ξ的分布列及數學期望.
(2)以這10人的樣本數據來估計整個班級的總體數據,若從該班任選3人,
【答案】
(1)解:設Ai表示所取3人中有i個人評價該教師為“優秀”,
至多1人評價該教師為“優秀”記為事件A,
則P(A)=P(A0)+P(A1)= ![]() =
= ![]() .
.
(2)解:由已知得ξ的可能取值為0,1,2,3,
P(ξ=0)=( ![]() )3=
)3= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)=( ![]() )3=
)3= ![]() ,
,
∴ξ的分布列為:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =0.9.
=0.9.
【解析】(1)設Ai表示所取3人中有i個人評價該教師為“優秀”,至多1人評價該教師為“優秀”記為事件A,由P(A)=P(A0)+P(A1),能求出至多有1人評價該教師是“優秀”的概率.(2)由已知得ξ的可能取值為0,1,2,3,分別求出相應的概率,由此能求出ξ的分布列及數學期望.


科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問部分職工,根據被訪問職工對該部門的評分,繪制頻率分布直方圖(如圖所示).
(1)求頻率分布表中①、②、③位置相應數據,并在答題紙上完成頻率分布直方圖;
組號 | 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 5 | 0.050 |
第2組 | [60,70) | ① | 0.350 |
第3組 | [70,80) | 30 | ② |
第4組 | [80,90) | 20 | 0.200 |
第5組 | [90,100] | 10 | 0.100 |
合計 | ③ | 1.00 | |
(2)為進一步了解情況,該企業決定在第3,4,5組中用分層抽樣抽取5名職工進行座談,求第3,4,5組中各自抽取的人數;
(3)求該樣本平均數 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某休閑農莊有一塊長方形魚塘ABCD,AB=50米,BC=25 ![]() 米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°.
米,為了便于游客休閑散步,該農莊決定在魚塘內建三條如圖所示的觀光走廊OE、EF和OF,考慮到整體規劃,要求O是AB的中點,點E在邊BC上,點F在邊AD上,且∠EOF=90°. 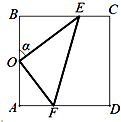
(1)設∠BOE=α,試將△OEF的周長l表示成α的函數關系式,并求出此函數的定義域;
(2)經核算,三條走廊每米建設費用均為4000元,試問如何設計才能使建設總費用最低并求出最低總費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對兩個變量y和x進行回歸分析,得到一組樣本數據:(x1 , y1),(x2 , y2),…,(xn , yn),則下列說法中不正確的是( )
A.由樣本數據得到的回歸方程 ![]() =
= ![]() x+
x+ ![]() 必過樣本中心(
必過樣本中心( ![]() ,
, ![]() )
)
B.殘差平方和越小的模型,擬合的效果越好
C.用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好
D.兩個隨機變量的線性相關性越強,相關系數的絕對值越接近于1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢驗學習情況,某培訓機構于近期舉辦一場競賽活動,分別從甲、乙兩班各抽取10名學員的成績進行統計分析,其成績的莖葉圖如圖所示(單位:分),假設成績不低于90分者命名為“優秀學員”.
(1)分別求甲、乙兩班學員成績的平均分(結果保留一位小數);
(2)從甲班4名優秀學員中抽取兩人,從乙班2名80分以下的學員中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分別是AB、BC邊的中點,沿DE將
,D、E分別是AB、BC邊的中點,沿DE將![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱錐F-ADEC的體積;
(Ⅱ)求證:平面ADF⊥平面ACF.
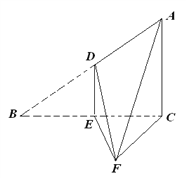
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ax﹣1,(a為實數),g(x)=lnx﹣x
(1)討論函數f(x)的單調區間;
(2)求函數g(x)的極值;
(3)求證:lnx<x<ex(x>0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,記
,記![]() ,若數列
,若數列![]() 滿足:“存在
滿足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,則稱數列
”,則稱數列![]() 具有性質
具有性質![]() .
.
(Ⅰ)若數列![]() 滿足
滿足![]() 判斷數列
判斷數列![]() 是否具有性質
是否具有性質![]() ?是否具有性質
?是否具有性質![]() ?
?
(Ⅱ)求證:“![]() 是有限集”是“數列
是有限集”是“數列![]() 具有性質
具有性質![]() ”的必要不充分條件;
”的必要不充分條件;
(Ⅲ)已知![]() 是各項為正整數的數列,且
是各項為正整數的數列,且![]() 既具有性質
既具有性質![]() ,又具有性質
,又具有性質![]() ,求證:存在整數
,求證:存在整數![]() ,使得
,使得![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,∠PAQ是村里一個小湖的一角,其中∠PAQ=60°.為了給村民營造豐富的休閑環境,村委會決定在直線湖岸AP與AQ上分別建觀光長廊AB與AC,其中AB是寬長廊,造價是800元/米;AC是窄長廊,造價是400元/米;兩段長廊的總造價預算為12萬元(恰好都用完);同時,在線段BC上靠近點B的三等分點D處建一個表演舞臺,并建水上通道AD(表演舞臺的大小忽略不計),水上通道的造價是600元/米. 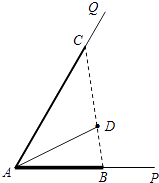
(1)若規劃寬長廊AB與窄長廊AC的長度相等,則水上通道AD的總造價需多少萬元?
(2)如何設計才能使得水上通道AD的總造價最低?最低總造價是多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com