
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問部分職工,根據被訪問職工對該部門的評分,繪制頻率分布直方圖(如圖所示).
(1)求頻率分布表中①、②、③位置相應數據,并在答題紙上完成頻率分布直方圖;
組號 | 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 5 | 0.050 |
第2組 | [60,70) | ① | 0.350 |
第3組 | [70,80) | 30 | ② |
第4組 | [80,90) | 20 | 0.200 |
第5組 | [90,100] | 10 | 0.100 |
合計 | ③ | 1.00 | |
(2)為進一步了解情況,該企業決定在第3,4,5組中用分層抽樣抽取5名職工進行座談,求第3,4,5組中各自抽取的人數;
(3)求該樣本平均數 ![]() .
.
【答案】
(1)解:5÷0.05=100,100×0.35=35,30÷100=0.030
故①35②0.300③100,其頻率分布直方圖如圖所示:

(2)解:第3,4,5組共有60名學生,第3,4,5組的頻數之比為:30:20:10=3:2:1,
則第3組抽取的人數為 ![]() 人;第4組為
人;第4組為 ![]() 人;第5組為
人;第5組為 ![]() 人.
人.
(3)解:樣本平均數 ![]()
【解析】(1)根據頻率= ![]() 即可求出,并畫出相應的圖象即可,(2)根據分層抽樣即可求出相對應的人數,(Ⅲ)根據平均數的定義即可求出.
即可求出,并畫出相應的圖象即可,(2)根據分層抽樣即可求出相對應的人數,(Ⅲ)根據平均數的定義即可求出.
【考點精析】本題主要考查了頻率分布直方圖和平均數、中位數、眾數的相關知識點,需要掌握頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息;⑴平均數、眾數和中位數都是描述一組數據集中趨勢的量;⑵平均數、眾數和中位數都有單位;⑶平均數反映一組數據的平均水平,與這組數據中的每個數都有關系,所以最為重要,應用最廣;⑷中位數不受個別偏大或偏小數據的影響;⑸眾數與各組數據出現的頻數有關,不受個別數據的影響,有時是我們最為關心的數據才能正確解答此題.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點E. 
(1)若D為AC的中點,證明:DE是⊙O的切線;
(2)若OA= ![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了體現國家“民生工程”,某市政府為保障居民住房,現提供一批經濟適用房.現有條件相同的甲、已、丙、丁四套住房供A、B、C三人自主申請,他們的申請是相互獨立的.
(1)求A、B兩人都申請甲套住房的概率;
(2)求A、B兩人不申請同一套住房的概率;
(3)設3名參加選房的人員中選擇甲套住房的人數為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把一顆骰子投擲兩次,記第一次出現的點數為a,第二次出現的點數為b.已知方程組 ![]() .
.
(1)求方程組只有一個解的概率;
(2)若方程組每個解對應平面直角坐標系中點P(x,y),求點P落在第四象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的圖象經過點(0,﹣1).
)的圖象經過點(0,﹣1).
(1)求函數f(x)的對稱軸方程及相鄰兩條對稱軸間的距離d;
(2)設α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1).當![]() 時,求
時,求![]() 的單調增區間;
的單調增區間;
(2)當![]() ,對于任意
,對于任意![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 的圖象始終在直線
的圖象始終在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校為測評班級學生對任課教師的滿意度,采用“100分制”打分的方式來計分.現從某班學生中隨機抽取10名,以下莖葉圖記錄了他們對某教師的滿意度分數(以十位數字為莖,個位數字為葉):
規定若滿意度不低于98分,測評價該教師為“優秀”.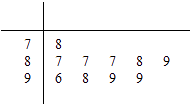
(1)求從這10人中隨機選取3人,至多有1人評價該教師是“優秀”的概率;
記ξ表示抽到評價該教師為“優秀”的人數,求ξ的分布列及數學期望.
(2)以這10人的樣本數據來估計整個班級的總體數據,若從該班任選3人,
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com