
【題目】傳統文化就是文明演化而匯集成的一種反映民族特質和風貌的民族文化,是民族歷史上各種思想文化、觀念形態的總體表征.教育部考試中心確定了2017年普通高考部分學科更注重傳統文化考核.某校為了了解高二年級中國數學傳統文化選修課的教學效果,進行了一次階段檢測,并從中隨機抽取80名同學的成績,然后就其成績分為A、B、C、D、E五個等級進行數據統計如下:
成績 | 人數 |
A | 9 |
B | 12 |
C | 31 |
D | 22 |
E | 6 |
根據以上抽樣調查數據,視頻率為概率.
(1)若該校高二年級共有1000名學生,試估算該校高二年級學生獲得成績為B的人數;
(2)若等級A、B、C、D、E分別對應100分、80分、60分、40分、20分,學校要求“平均分達60分以上”為“教學達標”,請問該校高二年級此階段教學是否達標?
(3)為更深入了解教學情況,將成績等級為A、B的學生中,按分層抽樣抽取7人,再從中任意抽取3名,求抽到成績為A的人數X的分布列與數學期望.
【答案】
(1)解:由于這80人中,有12名學生成績等級為B,
所以可以估計該校學生獲得成績等級為B的概率為 ![]() .
.
則該校高二年級學生獲得成績為B的人數約有1000× ![]() =150.
=150.
(2)解:由于這80名學生成績的平均分為:
![]() (9×100+12×80+31×60+22×40+6×20)=59.
(9×100+12×80+31×60+22×40+6×20)=59.
且59<60,因此該校高二年級此階段教學未達標
(3)解:成績為A、B的同學分別有9人,12人,
所以按分層抽樣抽取7人中成績為A的有3人,成績為B的有4人
則由題意可得:P(X=k)= ![]() ,k=0,1,2,3.
,k=0,1,2,3.
∴P(X=0)= ![]() ,P(X=1)=
,P(X=1)= ![]() ,P(X=2)=
,P(X=2)= ![]() ,P(X=3)=
,P(X=3)= ![]() .
.
所以EX=0+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]() .
.
【解析】(1)由于這80人中,有12名學生成績等級為B,所以可以估計該校學生獲得成績等級為B的概率為 ![]() ,即可得出該校高二年級學生獲得成績為B的人數.(2)由于這80名學生成績的平均分為:
,即可得出該校高二年級學生獲得成績為B的人數.(2)由于這80名學生成績的平均分為: ![]() (9×100+12×80+31×60+22×40+6×20).(3)成績為A、B的同學分別有9人,12人,所以按分層抽樣抽取7人中成績為A的有3人,成績為B的有4人.由題意可得:P(X=k)=
(9×100+12×80+31×60+22×40+6×20).(3)成績為A、B的同學分別有9人,12人,所以按分層抽樣抽取7人中成績為A的有3人,成績為B的有4人.由題意可得:P(X=k)= ![]() ,k=0,1,2,3.
,k=0,1,2,3.


科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”.利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出n的值為 . (參考數據:sin15°=0.2588,sin7.5°=0.1305) 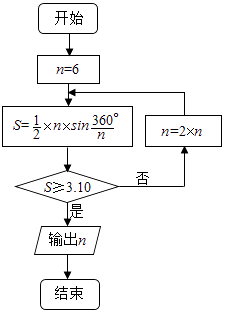
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列{an}中,a1=3,其前n項和為Sn , 等比數列{bn}的各項均為正數,b1=1,公比為q,且b2+S2=12,q= ![]() (Ⅰ)求an與bn;
(Ⅰ)求an與bn;
(Ⅱ)設數列{cn}滿足cn= ![]() ,求{cn}的前n項和Tn .
,求{cn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在邊長為4的菱形ABCD中,∠DAB=60°,點E,F分別是邊CD,CB的中點,AC∩EF=O,沿EF將△CEF翻折到△PEF,連接PA,PB,PD,得到如圖的五棱錐,且 ![]() .
. 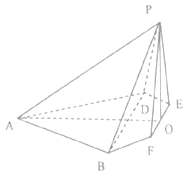
(1)求證:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=cos2ωx的圖象向右平移 ![]() 個單位,得到函數y=g(x)的圖象,若y=g(x)在
個單位,得到函數y=g(x)的圖象,若y=g(x)在 ![]() 上為減函數,則正實數ω的最大值為( )
上為減函數,則正實數ω的最大值為( )
A.![]()
B.1
C.![]()
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線E:y2=2px(p>0)的焦點為F,過F且垂直于x軸的直線與拋物線E交于A,B兩點,E的準線與x軸交于點C,△CAB的面積為4,以點D(3,0)為圓心的圓D過點A,B. (Ⅰ)求拋物線E和圓D的方程;
(Ⅱ)若斜率為k(|k|≥1)的直線m與圓D相切,且與拋物線E交于M,N兩點,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+m|+|2x﹣1|(m∈R) (I)當m=﹣1時,求不等式f(x)≤2的解集;
(II)設關于x的不等式f(x)≤|2x+1|的解集為A,且[ ![]() ,2]A,求實數m的取值范圍.
,2]A,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,AB=AC,D為△ABC外接圓劣弧 ![]() 上的點(不與點A,C重合),延長BD至E,延長AD交BC的延長線于F.
上的點(不與點A,C重合),延長BD至E,延長AD交BC的延長線于F. 
(1)求證:∠CDF=∠EDF;
(2)求證:ABACDF=ADFCFB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com