
【題目】已知橢圓![]() :
: ![]() 的兩個焦點與短軸的一個端點是直角三角形的三個頂點,直線
的兩個焦點與短軸的一個端點是直角三角形的三個頂點,直線![]() :
: ![]() 與橢圓
與橢圓![]() 有且只有一個公共點.
有且只有一個公共點.
(Ⅰ)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(Ⅱ)設![]() 是坐標原點,直線
是坐標原點,直線![]() 平行于
平行于![]() ,與橢圓
,與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,且與直線
,且與直線![]() 交于點
交于點![]() ,證明:存在常數
,證明:存在常數![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,點T坐標為(2,1);(Ⅱ)
,點T坐標為(2,1);(Ⅱ)![]() .
.
【解析】試題分析:本題考查橢圓的標準方程及其幾何性質,考查學生的分析問題、解決問題的能力和數形結合的思想.第(Ⅰ)問,利用直線和橢圓只有一個公共點,聯立方程,消去y得關于x的方程有兩個相等的實數根,解出b的值,從而得到橢圓E的方程;第(Ⅱ)問,利用橢圓的幾何性質,數形結合,根據根與系數的關系,進行求解.
試題解析:(Ⅰ)由已知, ![]() ,則橢圓E的方程為
,則橢圓E的方程為![]() .
.
由方程組 得
得![]() .①
.①
方程①的判別式為![]() ,由
,由![]() ,得
,得![]() ,
,
此時方程①的解為![]() ,
,
所以橢圓E的方程為![]() .
.
點T坐標為(2,1).
(Ⅱ)由已知可設直線![]() 的方程為
的方程為![]() ,
,
由方程組 可得
可得
所以P點坐標為(![]() ),
),![]() .
.
設點A,B的坐標分別為![]() .
.
由方程組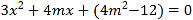 可得
可得![]() .②
.②
方程②的判別式為![]() ,由
,由![]() ,解得
,解得![]() .
.
由②得![]() .
.
所以 ,
,
同理![]() ,
,
所以![]()


![]() .
.
故存在常數![]() ,使得
,使得![]() .
.


科目:高中數學 來源: 題型:
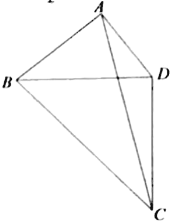
【題目】為了美化環境,某公園欲將一塊空地規劃建成休閑草坪,休閑草坪的形狀為如圖所示的四邊形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=
百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)當cos![]() =
=![]() 時,求小路AC的長度;
時,求小路AC的長度;
(2)當草坪ABCD的面積最大時,求此時小路BD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() :
:![]() (
(![]() 為參數,
為參數,![]() ),在以原點
),在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() :
:![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 有公共點,且直線
有公共點,且直線![]() 與曲線
與曲線![]() 的交點
的交點![]() 恰好在曲線
恰好在曲線![]() 與
與![]() 軸圍成的區域(不含邊界)內,求
軸圍成的區域(不含邊界)內,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了如下莖葉圖:
第一種生產方式 | 第二種生產方式 | |||||||||||||||||||
8 | 6 | 5 | 5 | 6 | 8 | 9 | ||||||||||||||
9 | 7 | 6 | 2 | 7 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 8 | ||||||
9 | 8 | 7 | 7 | 6 | 5 | 4 | 3 | 3 | 2 | 8 | 1 | 4 | 4 | 5 | ||||||
2 | 1 | 1 | 0 | 0 | 9 | 0 | ||||||||||||||
(1)根據莖葉圖判斷哪種生產方式的效率更高?并說明理由;
(2)求40名工人完成生產任務所需時間的中位數m,并將完成生產任務所需時間超過m和不超過m的工人數填入下面的列聯表:
超過m | 不超過m | 總計 | |
第一種生產方式 | |||
第二種生產方式 | |||
總計 |
(3)根據(2)中的列表,能否有99%的把握認為兩種生產方式的效率有差異?
附: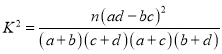 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市政府為做好![]() 會議接待服務工作,對可能遭受污染的某海產品在進入餐飲區前必須進行兩輪檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知該海產品第一輪檢測不合格的概率為
會議接待服務工作,對可能遭受污染的某海產品在進入餐飲區前必須進行兩輪檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知該海產品第一輪檢測不合格的概率為![]() ,第二輪檢測不合格的概率為
,第二輪檢測不合格的概率為![]() ,兩輪檢測是否合格相互沒有影響.
,兩輪檢測是否合格相互沒有影響.
(1)求該海產品不能銷售的概率.
(2)如果該海產品可以銷售,則每件產品可獲利40元;如果該海產品不能銷售,則每件產品虧損80元(即獲利-80元).已知一箱中有該海產品4件,記一箱該海產品獲利![]() 元,求
元,求![]() 的分布列,并求出數學期望
的分布列,并求出數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班隨機抽查了![]() 名學生的數學成績,分數制成如圖的莖葉圖,其中
名學生的數學成績,分數制成如圖的莖葉圖,其中![]() 組學生每天學習數學時間不足
組學生每天學習數學時間不足![]() 個小時,
個小時,![]() 組學生每天學習數學時間達到一個小時,學校規定
組學生每天學習數學時間達到一個小時,學校規定![]() 分及
分及![]() 分以上記為優秀,
分以上記為優秀,![]() 分及
分及![]() 分以上記為達標,
分以上記為達標,![]() 分以下記為未達標.
分以下記為未達標.

(1)根據莖葉圖完成下面的列聯表:
達標 | 未達標 | 總計 | |
| |||
| |||
總計 |
(2)判斷是否有![]() 的把握認為“數學成績達標與否”與“每天學習數學時間能否達到一小時”有關.
的把握認為“數學成績達標與否”與“每天學習數學時間能否達到一小時”有關.
參考公式與臨界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某外語學校的一個社團有7名同學,其中2人只會法語,2人只會英語,3人既會法語又會英語,現選派3人到法國的學校交流訪問.求:
(1)在選派的3人中恰有2人會法語的概率;
(2)求在選派的3人中既會法語又會英語的人數![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com