
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����![]() ��
��![]() ̎ȡ�ØOֵ��ֱ��
̎ȡ�ØOֵ��ֱ��![]() �c
�c![]() �ĈD��������(g��)��ͬ�Ľ��c(di��n)����
�ĈD��������(g��)��ͬ�Ľ��c(di��n)����![]() ��ȡֵ����.��
��ȡֵ����.��![]() �ĘO��ֵ��1����
�ĘO��ֵ��1����![]() ��ֵ.
��ֵ.
���𰸡���1����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��![]() ��
��![]() �����{(di��o)�p�^(q��)�g��
�����{(di��o)�p�^(q��)�g��![]() ����2��
����2��![]() ��
��![]() .
.
��������
��1����ú���(sh��)�Č�(d��o)��(sh��)![]() �����ӑՓ��������ú���(sh��)�Ć��{(di��o)�^(q��)�g��
�����ӑՓ��������ú���(sh��)�Ć��{(di��o)�^(q��)�g��
��2����![]() ��
��![]() ̎ȡ�ØOֵ�����
̎ȡ�ØOֵ�����![]() ���M(j��n)����ú���(sh��)�Ć��{(di��o)���c�Oֵ���Y(ji��)��ֱ��
���M(j��n)����ú���(sh��)�Ć��{(di��o)���c�Oֵ���Y(ji��)��ֱ��![]() �c����(sh��)
�c����(sh��)![]() �ĈD��������(g��)��ͬ�Ľ��c(di��n)���г�����ʽ���������,
�ĈD��������(g��)��ͬ�Ľ��c(di��n)���г�����ʽ���������,
��1�����}�⣬����(sh��)![]() ���t
���t![]() ��
��
��(d��ng)![]() �r(sh��)����(du��)
�r(sh��)����(du��)![]() ����
����![]() ��
��
���Ԯ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��![]() ��
��
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �����
�����![]() ��
��![]() ��
��
��![]() �����
�����![]() ��
��
���Ԯ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��![]() ��
��![]() ��
��
![]() ���{(di��o)�p�^(q��)�g��
���{(di��o)�p�^(q��)�g��![]() .
.
��2����?y��n)?/span>![]() ��
��![]() ̎ȡ�ØOֵ��
̎ȡ�ØOֵ��
����![]() ������
������![]() .
.
����![]() ��
��![]() .
.
��![]() �����
�����![]() ��
��![]() .
.
�ɣ�1�����ɵú���(sh��)![]() �Ć��{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��![]() ��
��![]() ��
��![]() ���{(di��o)�p�^(q��)�g��
���{(di��o)�p�^(q��)�g��![]() ��
��
���Ժ���(sh��)![]() ��
��![]() ̎ȡ�ØO��ֵ
̎ȡ�ØO��ֵ![]() ����
����![]() ̎ȡ�ØOСֵ
̎ȡ�ØOСֵ![]() .
.
��?y��n)�ֱ��![]() �c����(sh��)
�c����(sh��)![]() �ĈD��������(g��)��ͬ�Ľ��c(di��n)��
�ĈD��������(g��)��ͬ�Ľ��c(di��n)��
�Y(ji��)��![]() �Ć��{(di��o)�ԣ��ɵ�
�Ć��{(di��o)�ԣ��ɵ�![]() ��
��
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪����
�У���֪����![]() �ą���(sh��)���̞飺
�ą���(sh��)���̞飺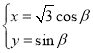 ����
����![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��ֱ��l�ĘO����(bi��o)���̞�
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��ֱ��l�ĘO����(bi��o)���̞�![]()
��1��������![]() ��ֱ��l��ֱ������(bi��o)���̣�
��ֱ��l��ֱ������(bi��o)���̣�
��2�����c(di��n)![]() ������
������![]() �ϣ����c(di��n)
�ϣ����c(di��n)![]() ��ֱ��l�ľ��x��С�����c(di��n)
��ֱ��l�ľ��x��С�����c(di��n)![]() ������(bi��o).
������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
![]() ��ʽ
��ʽ![]() �Ľ⼯��
�Ľ⼯��
![]() ������(sh��)
������(sh��)![]() ����Сֵ��
����Сֵ��![]() ������(sh��)
������(sh��)![]() ��
��![]() �M��
�M��![]() �����C
�����C![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �c
�c![]() �Sؓ(f��)���S����
�Sؓ(f��)���S����![]() ���x����
���x����![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2�����^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() ����
����![]() ��
��![]() ���c(di��n)���^�c(di��n)
���c(di��n)���^�c(di��n)![]() ���cֱ��
���cֱ��![]() ��ֱ��ֱ���cֱ��
��ֱ��ֱ���cֱ��![]() �ཻ���c(di��n)
�ཻ���c(di��n)![]() ����
����![]() ��ȡֵ������
��ȡֵ������![]() ȡ����Сֵ�r(sh��)ֱ��
ȡ����Сֵ�r(sh��)ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)��
�����ҽ��c(di��n)��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ���
�ϣ���![]() ��e�����ֵ��
��e�����ֵ��![]() �����L��6.
�����L��6.
��1����E�A![]() �ķ��̣�����E�A
�ķ��̣�����E�A![]() ���x���ʣ�
���x���ʣ�
��2����ֱ֪��![]() ��
��![]() �c�E�A
�c�E�A![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() ������
������![]() �S�ϴ����c(di��n)
�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �c
�c![]() ���c(di��n)���B���cֱ��
���c(di��n)���B���cֱ��![]() ��ֱ����(sh��)��(sh��)
��ֱ����(sh��)��(sh��)![]() ��ȡֵ����
��ȡֵ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijУ�ą��Ӹ���ģ�M��ԇ�ČW(xu��)�����S�C(j��)��ȡ60���W(xu��)�������䔵(sh��)�W(xu��)�ɿ�(��������(sh��))�ֳ�����[90,100)��[100,110)������[140,150)��õ����²����l�ʷֲ�ֱ���D���^��D�ε���Ϣ���ش����І��}��
���?j��n)?sh��)��[120,130)��(n��i)���l�ʣ����a(b��)ȫ�@��(g��)�l
�ʷֲ�ֱ���D��
�y(t��ng)Ӌ(j��)�����У�ͬһ�M��(sh��)��(j��)����ԓ�M�^(q��)�g�����c(di��n)
ֵ�����������(j��)�˹�Ӌ(j��)���ο�ԇ��ƽ���֣�
(3)�÷ӳ�ӵķ����ڷ�?j��n)?sh��)�Ξ�[110,130)�ČW(xu��)���г�ȡһ��(g��)������6�Ęӱ�����ԓ�ӱ�����һ��(g��)���w��������ȡ2��(g��)����������1���ڷ�?j��n)?sh��)��[120,130)��(n��i)�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ֪��![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() �Ľ���������ֱ��
�Ľ���������ֱ��![]() ��
��![]() �քe��ƽ��
�քe��ƽ��![]() ��ƽ��
��ƽ��![]() ��(n��i).
��(n��i).
���}![]() ��ֱ��
��ֱ��![]() ��
��![]() ��������һ�l�cֱ��
��������һ�l�cֱ��![]() �ཻ��
�ཻ��
���}![]() ��ֱ��
��ֱ��![]() ��
��![]() ��������һ�l�cֱ��
��������һ�l�cֱ��![]() �ཻ��
�ཻ��
���}![]() ��ֱ��
��ֱ��![]() ��
��![]() �����cֱ��
�����cֱ��![]() �ཻ.
�ཻ.
�t�������}���������}�Ğ飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ����߅��
����߅��![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ��
��![]() ��
��![]() �Ǿ���
�Ǿ���![]() �ϵĄ�(d��ng)�c(di��n)��
�ϵĄ�(d��ng)�c(di��n)��![]() �Ǿ���
�Ǿ���![]() �����c(di��n).
�����c(di��n).
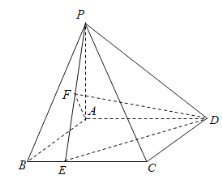
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǞ�
���ɽǞ�![]() ��
��
����![]() ���L��
���L��
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ֱ������![]() �������F
�������F![]() ��(g��u)�ɵĎ��w�У�
��(g��u)�ɵĎ��w�У� ![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��
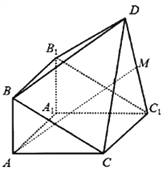
�������C�� ![]() ��
��
�����ھ���![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹֱ��
��ʹֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǞ�
���ɵĽǞ�![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ��f�����ɣ�
��ֵ���������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com