
【題目】已知橢圓C: ![]() 的離心率為
的離心率為 ![]() ,右焦點為F,點B(0,1)在橢圓C上.
,右焦點為F,點B(0,1)在橢圓C上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過點 ![]() 的直線交橢圓C于M,N兩點,交直線x=2于點P,設(shè)
的直線交橢圓C于M,N兩點,交直線x=2于點P,設(shè) ![]() ,
, ![]() ,求證:λ+μ為定值.
,求證:λ+μ為定值.
【答案】解:(Ⅰ)由點B(0,1)在橢圓C: ![]() 上,則
上,則 ![]() ,即b=1.
,即b=1.
又橢圓C的離心率為 ![]() ,則
,則 ![]() ,
,
由a2=b2+c2 , 得 ![]() .
.
∴橢圓C的方程為 ![]()
(Ⅱ)證明:由已知得F(1,0),直線MN的斜率存在.
設(shè)直線MN的方程為y=k(x﹣1),M(x1 , y1),N(x2 , y2),則P(2,k).
由 ![]() ,
, ![]() ,得
,得 ![]() ,
,
∴ ![]() ,.
,.
聯(lián)立 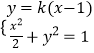 得(1+2k2)x2﹣4k2x+2k2﹣2=0.
得(1+2k2)x2﹣4k2x+2k2﹣2=0.
∴ ![]() ,
, ![]() .
.
∴ ![]() =
= ![]() =0,
=0,
∴λ+μ=0為定值
【解析】(Ⅰ)由題意b=1,利用橢圓的離心率即可求得a的值,求得橢圓方程;(Ⅱ)設(shè)直線MN的方程為y=k(x﹣1),代入橢圓方程,利用韋達定理及向量的坐標運算,即可證明λ+μ=0為定值.
【考點精析】本題主要考查了橢圓的標準方程的相關(guān)知識點,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能正確解答此題.
才能正確解答此題.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x-1+![]() x2-2,試利用基本初等函數(shù)的圖象,判斷f(x)有幾個零點,并利用零點存在性定理確定各零點所在的區(qū)間(各區(qū)間長度不超過1).
x2-2,試利用基本初等函數(shù)的圖象,判斷f(x)有幾個零點,并利用零點存在性定理確定各零點所在的區(qū)間(各區(qū)間長度不超過1).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某學(xué)校高三年級共![]() 名男生中隨機抽取
名男生中隨機抽取![]() 名測量身高,測量發(fā)現(xiàn)被測學(xué)生身高全部介于
名測量身高,測量發(fā)現(xiàn)被測學(xué)生身高全部介于![]() 和
和![]() 之間,將測量結(jié)果按如下方式分成八組,第一組
之間,將測量結(jié)果按如下方式分成八組,第一組![]() ;第二組
;第二組![]() ,
,![]() ,第八組
,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分,若第一組與第八組人數(shù)相同,第六組、第七組、第八組人數(shù)依次構(gòu)成等差數(shù)列.
,如圖是按上述分組方法得到的頻率分布直方圖的一部分,若第一組與第八組人數(shù)相同,第六組、第七組、第八組人數(shù)依次構(gòu)成等差數(shù)列.

(![]() )估計這所學(xué)校高三年級全體男生身高
)估計這所學(xué)校高三年級全體男生身高![]() 以上(含
以上(含![]() )的人數(shù).
)的人數(shù).
(![]() )求第六組、第七組的頻率并補充完整頻率分布直方圖.(鉛筆作圖并用中性筆描黑).
)求第六組、第七組的頻率并補充完整頻率分布直方圖.(鉛筆作圖并用中性筆描黑).
(![]() )若從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,記他們的身高分別為
)若從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,記他們的身高分別為![]() 、
、![]() ,求滿足
,求滿足![]() 的事件概率.
的事件概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ex﹣e﹣x , 下列命題正確的有 . (寫出所有正確命題的編號)
①f(x)是奇函數(shù);
②f(x)在R上是單調(diào)遞增函數(shù);
③方程f(x)=x2+2x有且僅有1個實數(shù)根;
④如果對任意x∈(0,+∞),都有f(x)>kx,那么k的最大值為2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知從橢圓![]() 的一個焦點看兩短軸端點所成視角為
的一個焦點看兩短軸端點所成視角為![]() ,且橢圓經(jīng)過
,且橢圓經(jīng)過![]() .
.
(1)求橢圓的方程;
(2)是否存在實數(shù)![]() ,使直線
,使直線![]() 與橢圓有兩個不同交點
與橢圓有兩個不同交點![]() ,且
,且![]() (
(![]() 為坐標原點),若存在,求出
為坐標原點),若存在,求出![]() 的值.不存在,說明理由.
的值.不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將函數(shù)f(x)=2 ![]() cos2x﹣2sinxcosx﹣
cos2x﹣2sinxcosx﹣ ![]() 的圖象向左平移t(t>0)個單位,所得圖象對應(yīng)的函數(shù)為奇函數(shù),則t的最小值為( )
的圖象向左平移t(t>0)個單位,所得圖象對應(yīng)的函數(shù)為奇函數(shù),則t的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,
, ![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心力為
的離心力為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,直線
為坐標原點,直線![]() :
: ![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
, ![]() 兩個不同的點,若存在實數(shù)
兩個不同的點,若存在實數(shù)![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發(fā)芽多少之間的關(guān)系,現(xiàn)在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每100顆種子浸泡后的發(fā)芽數(shù),得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
發(fā)芽數(shù)y/顆 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,記發(fā)芽的種子數(shù)分別為![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由線性回歸方程得到的估計數(shù)據(jù)與4月份所選5天的檢驗數(shù)據(jù)的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的. 請根據(jù)4月7日,4月15日與4月21日這三天的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并判定所得的線性回歸方程是否可靠?
,并判定所得的線性回歸方程是否可靠?
參考公式: 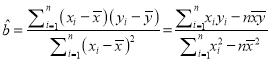 ,
, ![]()
參考數(shù)據(jù): ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() f.
f.
(1)如果函數(shù)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(2)在(1)的條件下,求函數(shù)![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(3)若不等式![]() 恒成立,求實數(shù)a的取值范圍.
恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com