【題目】已知函數f(x)＝x－1＋
x2－2，試利用基本初等函數的圖象，判斷f(x)有幾個零點，并利用零點存在性定理確定各零點所在的區間(各區間長度不超過1)．
【答案】3個零點分別在區間(－3，－2)，
，(1,2)內．
【解析】試題分析：本題是一個比較復雜的函數求零點的問題，通過轉化為兩個較熟悉的函數研究.容易得到兩個數有三個交點，所以有三個零點.零點的范圍不好確定，本題很巧妙地應用了零點定理，求出了個的范圍.這種方法值得好好體會.
試題解析：由f(x)=0，得
，令
，
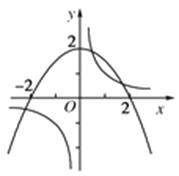
.分別畫出它們的圖象如圖，其中拋物線的頂點坐標為(0,2)，與x軸的交點為(-2,0)、(2,0)，
與
的圖象有3個交點，從而函數f(x)有3個零點．由f(x)的解析式知x≠0，f(x)的圖象在(-∞，0)和(0，+∞)上分別是連續不斷地曲線，且
即
，
.所以三個零點分別在區間（-3，-2），，（1,2）內.
口算小狀元口算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
（a＞b＞0）的離心率為
，以原點O為圓心，橢圓的短半軸長為半徑的圓與直線x﹣y+
=0相切．
（Ⅰ）求橢圓C的標準方程；
（Ⅱ）若直線l：y=kx+m與橢圓C相交于A、B兩點，且kOAkOB=﹣
，判斷△AOB的面積是否為定值？若為定值，求出定值；若不為定值，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2017屆陜西省西安市鐵一中學高三上學期第五次模擬考試數學（理）】已知函數
，其中常數
.
（Ⅰ）討論
在
上的單調性；
（Ⅱ）當
時，若曲線
上總存在相異兩點
，使曲線在
兩點處的切線互相平行，試求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在
中,根據下列條件解三角形,其中有兩個解的是（ ）
A. b="10," A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b="16," A=450
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】關于函數
有下列命題：
①函數
的圖象關于
軸對稱；
②在區間
上，函數
是減函數；
③在區間
上，函數
是增函數；
④函數
的值域是
.其中正確命題序號為____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
為實數.
（1）若關于
的不等式
的解集為
，求實數
的值；
（2）設
，當
時，求函數
的最小值（用
表示）；
（3）若關于
不等式
的解集中恰好有兩個整數解，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（1）求證： 
.
（2）某同學在一次研究性學習中發現，以下五個式子的值都等于同一個常數：
sin213°＋cos217°－sin13°cos17°；
sin215°＋cos215°－sin15°cos15°；
sin218°＋cos212°－sin18°cos12°；
sin2(－18°)＋cos248°－sin(－18°)cos48°；
sin2(－25°)＋cos255°－sin(－25°)cos55°.
①試從上述五個式子中選擇一個，求出這個常數；
②根據①的計算結果，將該同學的發現推廣為三角恒等式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
