
【題目】設![]() ,已知定義在R上的函數
,已知定義在R上的函數![]() 在區間
在區間![]() 內有一個零點
內有一個零點![]() ,
, ![]() 為
為![]() 的導函數.
的導函數.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)設![]() ,函數
,函數![]() ,求證:
,求證: ![]() ;
;
(Ⅲ)求證:存在大于0的常數![]() ,使得對于任意的正整數
,使得對于任意的正整數![]() ,且
,且![]() 滿足
滿足![]() .
.
【答案】(Ⅰ)增區間是![]() ,
, ![]() ,遞減區間是
,遞減區間是![]() .(Ⅱ)見解析;(III)見解析.
.(Ⅱ)見解析;(III)見解析.
【解析】試題分析:由于![]() 為
為![]() ,所以判斷
,所以判斷![]() 的單調性,需要對
的單調性,需要對![]() 二次求導,根據
二次求導,根據![]() 的導數的符號判斷函數的單調性,給出單調區間;由
的導數的符號判斷函數的單調性,給出單調區間;由![]() ,得
,得![]()
![]() ,.令函數
,.令函數![]() ,
, ![]() 分別求導證明.有關零點問題,利用函數的單調性了解函數的圖像情況,對極值作出相應的要求可控制零點的個數.
分別求導證明.有關零點問題,利用函數的單調性了解函數的圖像情況,對極值作出相應的要求可控制零點的個數.
試題解析:(Ⅰ)解:由![]() ,可得
,可得![]() ,
,
進而可得![]() .令
.令![]() ,解得
,解得![]() ,或
,或![]() .
.
當x變化時, ![]() 的變化情況如下表:
的變化情況如下表:
x |
|
|
|
| + | - | + |
| ↗ | ↘ | ↗ |
所以, ![]() 的單調遞增區間是
的單調遞增區間是![]() ,
, ![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(Ⅱ)證明:由![]() ,得
,得![]() ,
,
![]() .
.
令函數![]() ,則
,則![]() .由(Ⅰ)知,當
.由(Ⅰ)知,當![]() 時,
時, ![]() ,故當
,故當![]() 時,
時, ![]() ,
, ![]() 單調遞減;當
單調遞減;當![]() 時,
時, ![]() ,
, ![]() 單調遞增.因此,當
單調遞增.因此,當![]() 時,
時, ![]() ,可得
,可得![]() .
.
令函數![]() ,則
,則![]() .由(Ⅰ)知,
.由(Ⅰ)知, ![]() 在
在![]() 上單調遞增,故當
上單調遞增,故當![]() 時,
時, ![]() ,
, ![]() 單調遞增;當
單調遞增;當![]() 時,
時, ![]() ,
, ![]() 單調遞減.因此,當
單調遞減.因此,當![]() 時,
時, ![]() ,可得
,可得![]() .
.
所以, ![]() .
.
(III)證明:對于任意的正整數 ![]() ,
, ![]() ,且
,且![]() ,
,
令![]() ,函數
,函數![]() .
.
由(II)知,當![]() 時,
時, ![]() 在區間
在區間![]() 內有零點;
內有零點;
當![]() 時,
時, ![]() 在區間
在區間![]() 內有零點.
內有零點.
所以![]() 在
在![]() 內至少有一個零點,不妨設為
內至少有一個零點,不妨設為![]() ,則
,則![]() .
.
由(I)知![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() ,
,
于是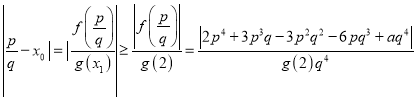 .
.
因為當![]() 時,
時, ![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在區間
在區間![]() 上除
上除![]() 外沒有其他的零點,而
外沒有其他的零點,而![]() ,故
,故![]() .
.
又因為![]() ,
, ![]() ,
, ![]() 均為整數,所以
均為整數,所以![]() 是正整數,
是正整數,
從而![]() .
.
所以![]() .所以,只要取
.所以,只要取![]() ,就有
,就有![]() .
.


科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且Sn=2an﹣2(n∈N*),數列{bn}滿足b1=1,且點P(bn , bn+1)(n∈N*)在直線y=x+2上.
(1)求數列{an}、{bn}的通項公式;
(2)求數列{anbn}的前n項和Dn;
(3)設cn=ansin2 ![]() ,求數列{cn}的前2n項和T2n .
,求數列{cn}的前2n項和T2n .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐中P﹣ABCD,底面ABCD為邊長為 ![]() 的正方形,PA⊥BD.
的正方形,PA⊥BD. 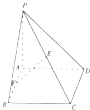
(1)求證:PB=PD;
(2)若E,F分別為PC,AB的中點,EF⊥平面PCD,求直線PB與平面PCD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上一點,
上一點, ![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
, ![]() 到
到![]() 的準線的距離為
的準線的距離為![]() ,且
,且![]() 的最小值為
的最小值為![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)直線![]() 交
交![]() 于點
于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() ,線段
,線段![]() 的中點分別為
的中點分別為![]() ,若
,若![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:直線
,求證:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線y=x2+mx–2與x軸交于A,B兩點,點C的坐標為(0,1).當m變化時,解答下列問題:
(1)能否出現AC⊥BC的情況?說明理由;
(2)證明過A,B,C三點的圓在y軸上截得的弦長為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在長方體ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M為B1C1上一點且B1M=2,點N在線段A1D上,A1D⊥AN. 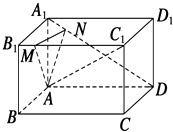
(1)求直線A1D與AM所成角的余弦值;
(2)求直線AD與平面ANM所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1927年德國漢堡大學的學生考拉茲提出一個猜想:對于每一個正整數,如果它是奇數,對它乘3再加1,如果它是偶數,對它除以2,這樣循環,最終結果都能得到1.該猜想看上去很簡單,但有的數學家認為“該猜想任何程度的解決都是現代數學的一大進步,將開辟全新的領域至于如此簡單明了的一個命題為什么能夠開辟一個全新的領域,這大概與它其中蘊含的奇偶歸一思想有關.如圖是根據考拉茲猜想設計的一個程序框圖,則①處應填寫的條件及輸出的結果![]() 分別為
分別為
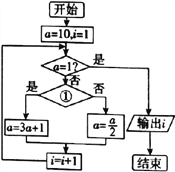
A. ![]() 是偶數?;6 B.
是偶數?;6 B. ![]() 是偶數?;8
是偶數?;8
C. ![]() 是奇數?;5 D.
是奇數?;5 D. ![]() 是奇數?;7
是奇數?;7
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設平面直角坐標系xOy中,曲線G:y= ![]() +
+ ![]() x﹣a2(x∈R),a為常數.
x﹣a2(x∈R),a為常數.
(1)若a≠0,曲線G的圖象與兩坐標軸有三個交點,求經過這三個交點的圓C的一般方程;
(2)在(1)的條件下,求圓心C所在曲線的軌跡方程;
(3)若a=0,已知點M(0,3),在y軸上存在定點N(異于點M)滿足:對于圓C上任一點P,都有 ![]() 為一常數,試求所有滿足條件的點N的坐標及該常數.
為一常數,試求所有滿足條件的點N的坐標及該常數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com