
【題目】已知{an}是各項都為正數的等比數列,其前n項和為Sn , 且S2=3,S4=15.
(1)求數列{an}的通項公式;
(2)若數列{bn}是等差數列,且b3=a3 , b5=a5 , 試求數列{bn}的前n項和Mn .
【答案】
(1)解:設等比數列{an}的公比為q,由題意分析知q≠1.
由S2=3,S4=15得: 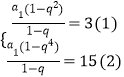 ,
,
![]() 得1+q2=5,得q2=4,由題意q>0,所以q=2.
得1+q2=5,得q2=4,由題意q>0,所以q=2.
將q=2代入(1)式得a1=1,
所以 ![]() .
.
(2)解:設數列{bn}的公差為d,
∵ ![]() ,
,
又{bn}為等差數列,∴b5=b3+(5﹣3)d,
即16=4+2d,解得d=6,
又由b3=b1+(3﹣1)d,得b1=﹣8
∴ ![]()
=3n2﹣11n.
【解析】(1)設等比數列{an}的公比為q,由題意分析知q≠1.運用等比數列的求和公式,解方程可得首項與公比,由等比數列的通項公式即可得到所求;(2)設數列{bn}的公差為d,運用等差數列的通項公式可得公差和首項,運用等差數列的求和公式,進而得到所求和.
【考點精析】利用等比數列的通項公式(及其變式)和數列的前n項和對題目進行判斷即可得到答案,需要熟知通項公式:![]() ;數列{an}的前n項和sn與通項an的關系
;數列{an}的前n項和sn與通項an的關系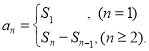 .
.


科目:高中數學 來源: 題型:
【題目】【2017福建三明5月質檢】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
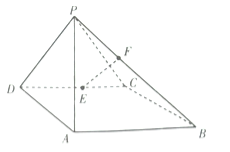
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定點![]() 的位置,使得直線
的位置,使得直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1:y=cos x,C2:y=sin (2x+![]() ),則下面結論正確的是
),則下面結論正確的是
A. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
B. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
C. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
D. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向左平移
倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個化肥廠生產甲種混合肥料1車皮、乙種混合肥料1車皮所需要的主要原料如表:
原料 | 磷酸鹽(單位:噸) | 硝酸鹽(單位:噸) |
甲 | 4 | 20 |
乙 | 2 | 20 |
現庫存磷酸鹽8噸、硝酸鹽60噸,計劃在此基礎上生產若干車皮的甲、乙兩種混合肥料.
(1)設x,y分別表示計劃生產甲、乙兩種肥料的車皮數,試列出x,y滿足的數學關系式,并畫出相應的平面區域;
(2)若生產1車皮甲種肥料,利潤為3萬元;生產1車皮乙種肥料,利潤為2萬元.那么分別生產甲、乙兩種肥料多少車皮,能夠產生最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=3ax2﹣2(a+b)x+b,(0≤x≤1)其中a>0,b為任意常數.
(I)若b= ![]() ,f(x)=|x﹣
,f(x)=|x﹣ ![]() |在x∈[0,1]有兩個不同的解,求實數a的范圍.
|在x∈[0,1]有兩個不同的解,求實數a的范圍.
(II)當|f(0)|≤2,|f(1)|≤2時,求|f(x)|的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com