
【題目】在如圖所示的直三棱柱![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 為正三角形,且
為正三角形,且![]() ,
,![]() 為
為![]() 上的一點,
上的一點,![]() ,求直線
,求直線![]() 與直線
與直線![]() 所成角的正切值.
所成角的正切值.
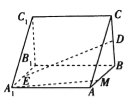
【答案】(Ⅰ)見解析(Ⅱ)![]()
【解析】
試題分析:(Ⅰ)取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() .,推導出
.,推導出![]() ,從而
,從而![]() 平面
平面![]() .
.
;再推導出![]() 平面
平面![]() ,進而平面
,進而平面![]() 平面
平面![]() .由此能證明
.由此能證明![]() 平面
平面![]() .(Ⅱ)推導出平面
.(Ⅱ)推導出平面![]()
![]() 平面
平面![]() .
.![]() 平面
平面![]() 取
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() 平面
平面![]() ,又
,又![]() ,可得
,可得![]() ,所以
,所以![]() 即為直線
即為直線![]() 與直線
與直線![]() 所成角.,由此能求出直線
所成角.,由此能求出直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
試題解析:(Ⅰ)取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() .
.
在![]() 中,因為
中,因為![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,所以
的中點,所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
在矩形![]() 中,因為
中,因為![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,故
,故 ![]() 平面
平面![]() ;
;
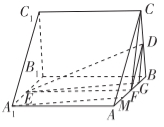
(Ⅱ)因為三棱柱![]() 為直三棱柱,所以平面
為直三棱柱,所以平面![]()
![]() 平面
平面![]() .
.
連接![]() ,因為
,因為![]() 為正三角形,
為正三角形,![]() 為
為![]() 中點,所以
中點,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() 平面
平面![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
所以![]() 即為直線
即為直線![]() 與直線
與直線![]() 所成角.
所成角.
設![]() ,在
,在![]() 中,
中,![]() ,
,![]() .
.
所以![]() .
.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(1)將曲線![]() 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的![]() 倍后得到曲線
倍后得到曲線![]() .試寫出直線
.試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程:
的參數方程:
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣![]() ﹣(a+2)lnx,其中實數a≥0.
﹣(a+2)lnx,其中實數a≥0.
(1)若a=0,求函數f(x)在x∈[1,3]上的最值;
(2)若a>0,討論函數f(x)的單調性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三次函數![]() ,
,
(1)若函數![]() 過點
過點![]() 且在點
且在點![]() 處的切線方程是
處的切線方程是![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(2)在(1)的條件下,若對于區間![]() 上任意兩個自變量的值
上任意兩個自變量的值![]() ,
,
都有![]() ,求實數
,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市統計局就2015年畢業大學生的月收入情況調查了10000人,并根據所得數據畫出樣本的頻率分布直方圖所示,每個分組包括左端點,不包括右端點,如第一組表示![]() .
.
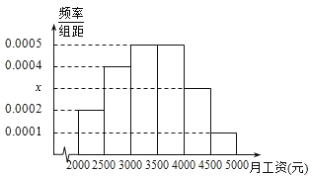
(1)求畢業大學生月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析大學生的收入與所學專業、性別等方面的關系,必須按月收入再從這10000人中按分層抽樣方法抽出100人作進一步分析,則月收入在![]() 的這段應抽取多少人?
的這段應抽取多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com