
【題目】設函數![]() .
.
(1)若函數![]() 是奇函數,求實數
是奇函數,求實數![]() 的值;
的值;
(2)若對任意的實數![]() ,函數
,函數![]() (
(![]() 為實常數)的圖象與函數
為實常數)的圖象與函數![]() 的圖象總相切于一個定點.
的圖象總相切于一個定點.
① 求![]() 與
與![]() 的值;
的值;
② 對![]() 上的任意實數
上的任意實數![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)0;(2)①![]() ;②
;②![]() .
.
【解析】試題分析:
(1)由奇函數的 定義得到關于實數a的方程,解方程可得a=0;
(2)由導函數研究函數的 切線可得切點為![]() ,切線的方程為
,切線的方程為![]() ,則
,則![]() .
.
(3)由題意分類討論 ![]() 和
和![]() 兩種情況可得實數
兩種情況可得實數![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:
解:(1)因為函數![]() 是奇函數,所以
是奇函數,所以![]() 恒成立,
恒成立,
即![]() ,得
,得![]() 恒成立,
恒成立,
![]() .
.
(2)①![]() ,設切點為
,設切點為![]() ,
,
則切線的斜率為![]() ,
,
據題意![]() 是與
是與![]() 無關的常數,故
無關的常數,故![]() ,切點為
,切點為![]() , 由點斜式得切線的方程為
, 由點斜式得切線的方程為![]() ,即
,即![]() ,故
,故![]() .
.
② 當![]() 時,對任意的
時,對任意的![]() ,都有
,都有![]() ;
;
當![]() 時,對任意的
時,對任意的![]() ,都有
,都有![]() ;
;
故![]() 對
對![]() 恒成立,或
恒成立,或![]() 對
對![]() 恒成立.
恒成立.
而![]() ,設函數
,設函數![]() .
.
則![]() 對
對![]() 恒成立,或
恒成立,或![]() 對
對![]() 恒成立,
恒成立, ![]() ,
,
![]() 當
當![]() 時,
時, ![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上遞增,
上遞增, ![]() ,
,
故![]() 在
在![]() 上恒成立,符合題意.
上恒成立,符合題意. ![]() 當
當![]() 時,令
時,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 在
在![]() 上遞減,所以
上遞減,所以![]() ,
,
而![]() 設函數
設函數![]() ,
,
則![]() ,
, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上遞增,
上遞增, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上遞增,
上遞增, ![]() 恒成立,
恒成立,
即![]() ,而
,而![]() ,不合題意.
,不合題意.
綜上![]() ,知實數
,知實數![]() 的取值范圍
的取值范圍![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
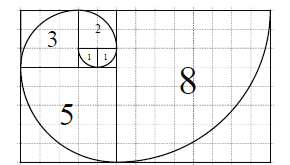
【題目】斐波那契數列![]() 滿足:
滿足: ![]() .若將數列的每一項按照下圖方法放進格子里,每一小格子的邊長為1,記前
.若將數列的每一項按照下圖方法放進格子里,每一小格子的邊長為1,記前![]() 項所占的格子的面積之和為
項所占的格子的面積之和為![]() ,每段螺旋線與其所在的正方形所圍成的扇形面積為
,每段螺旋線與其所在的正方形所圍成的扇形面積為![]() ,則下列結論錯誤的是( )
,則下列結論錯誤的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
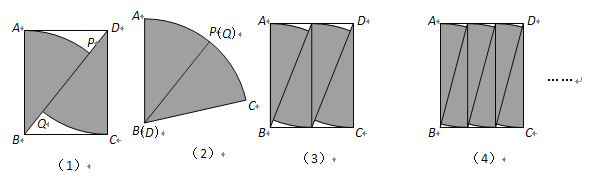
【題目】矩形紙片ABCD中,AB=10cm,BC=8cm.將其按圖(1)的方法分割,并按圖(2)的方法焊接成扇形;按圖(3)的方法將寬BC ![]() 等分,把圖(3)中的每個小矩形按圖(1)分割并把4個小扇形焊接成一個大扇形;按圖(4)的方法將寬BC
等分,把圖(3)中的每個小矩形按圖(1)分割并把4個小扇形焊接成一個大扇形;按圖(4)的方法將寬BC ![]() 等分,把圖(4)中的每個小矩形按圖(1)分割并把6個小扇形焊接成一個大扇形;……;依次將寬BC
等分,把圖(4)中的每個小矩形按圖(1)分割并把6個小扇形焊接成一個大扇形;……;依次將寬BC ![]() 等分,每個小矩形按圖(1)分割并把
等分,每個小矩形按圖(1)分割并把![]() 個小扇形焊接成一個大扇形.當n
個小扇形焊接成一個大扇形.當n![]() 時,最后拼成的大扇形的圓心角的大小為 ( )
時,最后拼成的大扇形的圓心角的大小為 ( )
A. 小于![]() B. 等于
B. 等于![]() C. 大于
C. 大于![]() D. 大于
D. 大于![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記函數f(x)=log2(2x﹣3)的定義域為集合M,函數g(x)=![]() 的定義域為集合N.求:
的定義域為集合N.求:
(Ⅰ)集合M,N;
(Ⅱ)集合M∩N,R(M∪N).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]()
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() , 與橢圓交于另一個點
, 與橢圓交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點(
兩點(![]() ),若
),若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]()
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() , 與橢圓交于另一個點
, 與橢圓交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點(
兩點(![]() ),若
),若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一長為24米的籬笆,一面利用墻(墻最大長度是10米)圍成一個矩形花圃,設該花圃寬AB為x米,面積是y平方米,
(1)求出y關于x的函數解析式,并指出x的取值范圍;
(2)當花圃一邊AB為多少米時,花圃面積最大?并求出這個最大面積?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸與極軸建立極坐標系,已知曲線
軸的正半軸與極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com