
【題目】設函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,是否存在整數
時,是否存在整數![]() ,使不等式
,使不等式![]() 恒成立?若存在,求整數
恒成立?若存在,求整數![]() 的值;若不存在,則說明理由;
的值;若不存在,則說明理由;
(3)關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個相異實根,求實數
上恰有兩個相異實根,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】試題分析:(1)求函數的定義域、導函數,由![]() ,
, ![]() 可求單調區間;(2)由(1)可求函數
可求單調區間;(2)由(1)可求函數![]() 在
在![]() 上的單調性,進而求最大值、最小值。由不等式
上的單調性,進而求最大值、最小值。由不等式![]() 恒成立,得
恒成立,得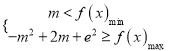 ,解不等式組可求m的范圍;(3)構造函數
,解不等式組可求m的范圍;(3)構造函數![]() =
= ![]() ,求其導函數,進而求單調性、最大、最小值,由關于
,求其導函數,進而求單調性、最大、最小值,由關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個相異實根,轉化為
上恰有兩個相異實根,轉化為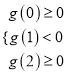 ,進而不等式組求實數
,進而不等式組求實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)由![]() 得函數
得函數![]() 的定義域為
的定義域為![]() .
.
![]()
![]() .
.
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
∴函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)由(1)知, ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.∴
上單調遞增.∴![]() .
.
又![]() ,
, ![]() ,且
,且![]() ,
,
∴![]() 時,
時, ![]() .
.
∵不等式![]() 恒成立,
恒成立,
∴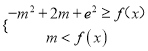 ,
,
即![]()
![]()
![]() .
.
∵![]() 是整數,∴
是整數,∴![]() .
.
∴存在整數![]() ,使不等式
,使不等式![]() 恒成立.
恒成立.
(3)由![]() ,得
,得![]() .
.
令![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
由![]() ,得
,得![]() ;由
;由![]() 得
得![]() .
.
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
∵方程![]() 在
在![]() 上恰有兩個相異實根,
上恰有兩個相異實根,
∴函數![]() 在
在![]() 和
和![]() 上各有一個零點.
上各有一個零點.
∴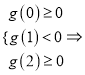
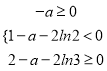
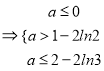
![]() .
.
∴實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某校對高一年級學生寒假參加社區服務的次數進行了統計,隨機抽取了![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:
名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
(2)如果用分層抽樣的方法從樣本服務次數在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務次數都在
的人中共抽取6人,再從這6人中選2人,求2人服務次數都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠有容量300噸的水塔一個,每天從早六點到晚十點供應生活和生產用水,已知:該廠生活用水每小時10噸,工業用水總量![]() (噸)與時間
(噸)與時間![]() (單位:小時,規定早晨六點時
(單位:小時,規定早晨六點時![]() )的函數關系為
)的函數關系為![]() ,水塔的進水量有10級,第一級每小時進水10噸,以后每提高一級, 進水量增加10噸.若某天水塔原有水100噸,在供應同時打開進水管.問該天進水量應選擇幾級,既能保證該廠用水(即水塔中水不空),又不會使水溢出?
,水塔的進水量有10級,第一級每小時進水10噸,以后每提高一級, 進水量增加10噸.若某天水塔原有水100噸,在供應同時打開進水管.問該天進水量應選擇幾級,既能保證該廠用水(即水塔中水不空),又不會使水溢出?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如下圖所示,其中主視圖與左視圖是腰長為6的等腰直角三角形,俯視圖是正方形.

(Ⅰ)請畫出該幾何體的直觀圖,并求出它的體積;
(Ⅱ)用多少個這樣的幾何體可以拼成一個棱長為6的正方體ABCD—A1B1C1D1? 如何組拼?試證明你的結論;
(Ⅲ)在(Ⅱ)的情形下,設正方體ABCD—A1B1C1D1的棱CC1的中點為E, 求平面AB1E與平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)若函數![]() 在
在![]() 上單調遞減,求實數
上單調遞減,求實數![]() 的取值范圍;
的取值范圍;
(3)在函數![]() 的圖象上是否存在不同的兩點
的圖象上是否存在不同的兩點![]() ,使線段
,使線段![]() 的中點的橫坐標
的中點的橫坐標![]() 與直線
與直線![]() 的斜率
的斜率![]() 之間滿足
之間滿足![]() ?若存在,求出
?若存在,求出![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題共13分)根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示
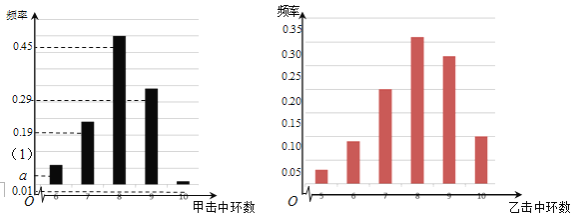
(1)求上圖中![]() 的值;
的值;
(2)甲隊員進行一次射擊,求命中環數大于7環的概率(頻率當作概率使用);
(3)由上圖判斷甲、乙兩名隊員中,哪一名隊員的射擊成績更穩定(結論不需證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于x的一元二次方程x2+2ax+b2=0.
(1)若a是從0,1,2,3四個數中任取的一個數,b是從0,1,2三個數中任取的一個數,求上述方程有實根的概率.
(2)若a是從區間[0,3]任取的一個數,b是從區間[0,2]任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com