
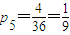 .…(8分)
.…(8分) .…(12分)
.…(12分)

 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2010年廣東省高考沖刺強化訓練試卷二文科數學 題型:解答題
(本小題滿分12分)
同時擲兩個骰子,計算:
(Ⅰ)一共有多少種不同的結果?
(Ⅱ)其中向上的點數之和是5的結果有多少種?概率是多少?
(III)向上的點數之和小于5的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com