
分析 (1)由題意,$\overrightarrow{AB}∥\overrightarrow{BC}$,$\overrightarrow{OA}⊥$$\overrightarrow{OB}$,利用平面向量的坐標表示列出方程組,求出m、n;
(2)由三角形重心的性質,結合平面向量的坐標運算,利用夾角公式即可求出答案.
解答 解:(1)因為三點A,B,C在一條直線上,所以$\overrightarrow{AB}∥\overrightarrow{BC}$,
又$\overrightarrow{AB}=(n+3,2-m)$,$\overrightarrow{BC}=(7-n,1)$,
所以n+3=(7-n)(2-m),①
因為$\overrightarrow{OA}⊥$$\overrightarrow{OB}$,所以-3n+3(m+1)=0,即n=m+1,②
由①、②解得$\left\{\begin{array}{l}m=8\\ n=9\end{array}\right.$,或$\left\{\begin{array}{l}m=1\\ n=2\end{array}\right.$;
(2)因為G為△OAC的重心,且$\overrightarrow{OG}=\frac{2}{3}\overrightarrow{OB}$,
所以點B為線段AC的中點,
所以m=1,n=2;
所以$\overrightarrow{OA}=(-3,2)$,$\overrightarrow{OC}=(7,4)$,
因此$cos∠AOC=\frac{{\overrightarrow{OA}•\overrightarrow{OC}}}{{|\overrightarrow{OA}|•|\overrightarrow{OC}|}}=\frac{-21+8}{{\sqrt{13}•\sqrt{65}}}=-\frac{{\sqrt{5}}}{5}$.
點評 本題考查了平面向量的坐標表示以及三角形重心的性質和平面向量的夾角公式問題,是綜合題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
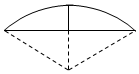 《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}×$(弦×矢+矢2),弧田(如圖)由圓弧和其所對弦圍城,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角$\frac{2π}{3}$,半徑為6米的弧田,按照上述經驗公式計算所得弧田面積約是($\sqrt{3}≈1.73$)( )
《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}×$(弦×矢+矢2),弧田(如圖)由圓弧和其所對弦圍城,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角$\frac{2π}{3}$,半徑為6米的弧田,按照上述經驗公式計算所得弧田面積約是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
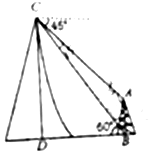 如圖所示,在塔底B測得山頂C的仰角為60°,在山頂測得塔頂A的仰角為45°,已知塔高AB=20米,則山高DC=10(3+$\sqrt{3}$)米.
如圖所示,在塔底B測得山頂C的仰角為60°,在山頂測得塔頂A的仰角為45°,已知塔高AB=20米,則山高DC=10(3+$\sqrt{3}$)米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com