
【題目】隨著網絡時代的進步,流量成為手機的附帶品,人們可以利用手機隨時隨地的瀏覽網頁,聊天,看視頻,因此,社會上產生了很多低頭族.某研究人員對該地區18∽50歲的5000名居民在月流量的使用情況上做出調查,所得結果統計如下圖所示:
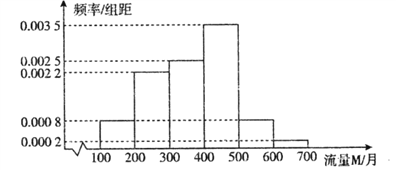
(Ⅰ)以頻率估計概率,若在該地區任取3位居民,其中恰有![]() 位居民的月流量的使用情況
位居民的月流量的使用情況
在300M∽400M之間,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)經過數據分析,在一定的范圍內,流量套餐的打折情況![]() 與其日銷售份數
與其日銷售份數![]() 成線性相關
成線性相關
關系,該研究人員將流量套餐的打折情況![]() 與其日銷售份數
與其日銷售份數![]() 的結果統計如下表所示:
的結果統計如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
銷售份數 | 50 | 85 | 115 | 140 | 160 |
試建立![]() 關于
關于![]() 的的回歸方程.
的的回歸方程.
附注:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
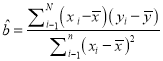 ,
, ![]()
【答案】(Ⅰ)0.75;(Ⅱ)369M;(Ⅲ) ![]() .
.
【解析】試題分析:(I)直接根據二項分布的期望公式求解即可;(II)根據頻率分布直方圖中數據,每組數據中間值與縱坐標的乘積之和即是被抽查的居民使用流量的平均值;(Ⅲ)先根據平均值公式求出樣本中心點的坐標,利用公式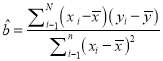 求出
求出![]() ,樣本中心點坐標代入回歸方程可得
,樣本中心點坐標代入回歸方程可得![]() ,從而可得結果.
,從而可得結果.
試題解析:(Ⅰ)依題意, ![]() ∽
∽![]() ,故
,故![]() ;
;
(Ⅱ)依題意,所求平均數為![]() 故所用流量的平均值為
故所用流量的平均值為![]() ;
;
(Ⅲ)由題意可知![]() ,
,
![]() ,
,
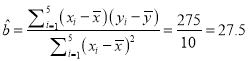 ,
,
![]() 所以,
所以, ![]() 關于
關于![]() 的回歸方程為:
的回歸方程為: ![]() .
.
【方法點晴】本題主要考查二項分布的期望公式、直方圖的應用和線性回歸方程的求法,屬于難題.求回歸直線方程的步驟:①依據樣本數據畫出散點圖,確定兩個變量具有線性相關關系;②計算![]() 的值;③計算回歸系數
的值;③計算回歸系數![]() ;④寫出回歸直線方程為
;④寫出回歸直線方程為![]() ; 回歸直線過樣本點中心
; 回歸直線過樣本點中心![]() 是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.
是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
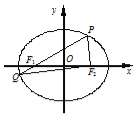
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)的左、右焦點分別為F1,F2,P為橢圓上一點(在x軸上方),連結PF1并延長交橢圓于另一點Q,設
(a>b>0)的左、右焦點分別為F1,F2,P為橢圓上一點(在x軸上方),連結PF1并延長交橢圓于另一點Q,設![]() =λ
=λ![]() .
.
(1)若點P的坐標為(1,![]() ),且△PQF2的周長為8,求橢圓C的方程;
),且△PQF2的周長為8,求橢圓C的方程;
(2)若PF2垂直于x軸,且橢圓C的離心率e∈[![]() ,
,![]() ],求實數λ的取值范圍.
],求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在圓
在圓![]() 上,
上, ![]() 的坐標分別為
的坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點
于點![]()
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設圓![]() 與點
與點![]() 的軌跡
的軌跡![]() 交于不同的四個點
交于不同的四個點![]() ,求四邊形
,求四邊形![]() 的面積的最大值及相應的四個點的坐標.
的面積的最大值及相應的四個點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱錐C-ADE的體積;
(II)求證:平面ACE⊥平面CDE;
(III)在線段DE上是否存在一點F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() 是曲線
是曲線![]() 與直線
與直線![]() :
: ![]() (
(![]() )的交點(異于原點
)的交點(異于原點![]() ).
).
(1)寫出![]() ,
, ![]() 的直角坐標方程;
的直角坐標方程;
(2)求過點![]() 和直線
和直線![]() 垂直的直線
垂直的直線![]() 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為常數,
為常數, ![]() 為自然對數的底數.
為自然對數的底數.
(1)若![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,求
,求![]() 的值;
的值;
(2)當![]() 時,判斷方程
時,判斷方程![]() 是否有實根?若無實根請說明理由,若有實根請給出根的個數.
是否有實根?若無實根請說明理由,若有實根請給出根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子里有編號為![]() 的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
甲說:“我無法確定.”
乙說:“我也無法確定.”
甲聽完乙的回答以后,甲又說:“我可以確定了.”
根據以上信息, 你可以推斷出抽取的兩球中
A. 一定有3號球 B. 一定沒有3號球 C. 可能有5號球 D. 可能有6號球
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=-f′(0)ex+2x,點P為曲線y=f(x)在點(0,f(0))處的切線l上的一點,點Q在曲線y=ex上,則|PQ|的最小值為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com