
【題目】龍虎山花語世界位于龍虎山主景區(qū)排衙峰下,是一座獨(dú)具現(xiàn)代園藝風(fēng)格的花卉公園,園內(nèi)匯集了![]() 余種花卉苗木,一年四季姹紫嫣紅花香四溢.花園景觀融合法、英、意、美、日、中六大經(jīng)典園林風(fēng)格,景觀設(shè)計(jì)唯美新穎,玫瑰花園、香草花溪、臺地花海、植物迷宮、兒童樂園等景點(diǎn)錯落有致,交相呼應(yīng)又自成一體,是世界園藝景觀的大展示.該景區(qū)自
余種花卉苗木,一年四季姹紫嫣紅花香四溢.花園景觀融合法、英、意、美、日、中六大經(jīng)典園林風(fēng)格,景觀設(shè)計(jì)唯美新穎,玫瑰花園、香草花溪、臺地花海、植物迷宮、兒童樂園等景點(diǎn)錯落有致,交相呼應(yīng)又自成一體,是世界園藝景觀的大展示.該景區(qū)自![]() 年春建成,試運(yùn)行以來,每天游人如織,郁金香、向日葵、虞美人等賞花旺季日入園人數(shù)最高達(dá)萬人.
年春建成,試運(yùn)行以來,每天游人如織,郁金香、向日葵、虞美人等賞花旺季日入園人數(shù)最高達(dá)萬人.
某學(xué)校社團(tuán)為了解進(jìn)園旅客的具體情形以及采集旅客對園區(qū)的建議,特別在![]() 年
年![]() 月
月![]() 日賞花旺季對進(jìn)園游客進(jìn)行取樣調(diào)查,從當(dāng)日
日賞花旺季對進(jìn)園游客進(jìn)行取樣調(diào)查,從當(dāng)日![]() 名游客中抽取
名游客中抽取![]() 人進(jìn)行統(tǒng)計(jì)分析,結(jié)果如下:
人進(jìn)行統(tǒng)計(jì)分析,結(jié)果如下:
年齡 | 頻數(shù) | 頻率 | 男 | 女 |
|
|
|
|
|
| ① | ② | ③ | ④ |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計(jì) |
|
|
|
|
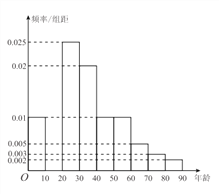
(I)完成表一中的空位①~④,并作答題紙中補(bǔ)全頻率分布直方圖,并估計(jì)![]() 年
年![]() 月
月![]() 日當(dāng)日接待游客中
日當(dāng)日接待游客中![]() 歲以下的游戲的人數(shù).
歲以下的游戲的人數(shù).
(II)完成表二,并判斷能否有![]() 的把握認(rèn)為在觀花游客中“年齡達(dá)到
的把握認(rèn)為在觀花游客中“年齡達(dá)到![]() 歲以上”與“性別”相關(guān);
歲以上”與“性別”相關(guān);
(表二)
|
| 合計(jì) | |
男生 | |||
女生 | |||
合計(jì) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式: 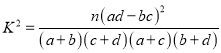 ,其中
,其中![]() )
)
(III)按分層抽樣(分![]() 歲以上與
歲以上與![]() 歲以下兩層)抽取被調(diào)查的
歲以下兩層)抽取被調(diào)查的![]() 位游客中的
位游客中的![]() 人作為幸運(yùn)游客免費(fèi)領(lǐng)取龍虎山內(nèi)部景區(qū)門票,再從這
人作為幸運(yùn)游客免費(fèi)領(lǐng)取龍虎山內(nèi)部景區(qū)門票,再從這![]() 人中選取
人中選取![]() 人接受電視臺采訪,設(shè)這
人接受電視臺采訪,設(shè)這![]() 人中年齡在
人中年齡在![]() 歲以上(含
歲以上(含![]() 歲)的人數(shù)為
歲)的人數(shù)為![]() ,求
,求![]() 的分布列.
的分布列.
【答案】(1)6000;(2)見解析;(3)見解析.
【解析】試題分析:(I)由頻率分布表的性質(zhì)能完成表(—),從而能完成頻率分布直方圖,進(jìn)而求出![]() 歲以下頻率,由此以頻率作為概率,能估計(jì)2017 年7月1日當(dāng)日接待游客中
歲以下頻率,由此以頻率作為概率,能估計(jì)2017 年7月1日當(dāng)日接待游客中![]() 歲以下人數(shù);(II)完成表格,求出
歲以下人數(shù);(II)完成表格,求出![]() ,從而得到?jīng)]有
,從而得到?jīng)]有![]() 的把握認(rèn)為在觀花游客中“年齡達(dá)到
的把握認(rèn)為在觀花游客中“年齡達(dá)到![]() 以上”與“性別”有關(guān);(III)由分層抽樣應(yīng)從這
以上”與“性別”有關(guān);(III)由分層抽樣應(yīng)從這![]() 人中抽取
人中抽取![]() 以上人數(shù):
以上人數(shù): ![]() ,
, ![]() 以下人數(shù)
以下人數(shù)![]() 的取值可能
的取值可能![]() ,分別求出相應(yīng)的概率,由此能求出
,分別求出相應(yīng)的概率,由此能求出 ![]() 的分布列.
的分布列.
試題解析:(I)完成表(一): ![]() .
.
完成以下頻率分布直方圖:
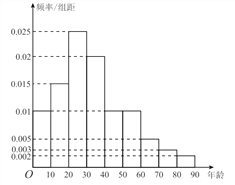
因?yàn)槟挲g在![]() 歲以下的頻率為
歲以下的頻率為![]() ,
,
以頻率作為概率,估計(jì)![]() 年
年![]() 月
月![]() 日當(dāng)日接待游客中
日當(dāng)日接待游客中![]() 歲以下的人數(shù)為
歲以下的人數(shù)為![]() .
.
(II)完成![]() 列聯(lián)表如下:
列聯(lián)表如下:
|
| 合計(jì) | |
男生 |
|
|
|
女生 |
|
|
|
合計(jì) |
|
|
|
![]() 的觀測值
的觀測值![]() ,
,
所以沒有![]() 的把握認(rèn)為在觀花游客中“年齡達(dá)到
的把握認(rèn)為在觀花游客中“年齡達(dá)到![]() 歲以上”與“性別”相關(guān).
歲以上”與“性別”相關(guān).
(III)由分層抽樣應(yīng)從這![]() 人中抽取到
人中抽取到![]() 歲以上的人的人數(shù)為
歲以上的人的人數(shù)為![]() 人,
人,
![]() 歲以下的人的人數(shù)為
歲以下的人的人數(shù)為![]() 人,
人,
故![]() 的所有可能的取值為
的所有可能的取值為![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
故![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù),求函數(shù)
為自然對數(shù)的底數(shù),求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 既有極大值,又有極小值,求實(shí)數(shù)
既有極大值,又有極小值,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 為何值時,
為何值時, ![]() 軸為曲線
軸為曲線![]() 的切線;
的切線;
(2)用![]() 表示
表示![]() 中的最小值,設(shè)函數(shù)
中的最小值,設(shè)函數(shù)![]() ,討論
,討論![]() 零點(diǎn)的個數(shù).
零點(diǎn)的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)是定義在實(shí)數(shù)集R上的函數(shù),且y=f(x+1)是偶函數(shù),當(dāng)x≥1時,f(x)=2x﹣1,則f( ![]() ),f(
),f( ![]() ),f(
),f( ![]() )的大小關(guān)系是( )
)的大小關(guān)系是( )
A.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
B.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )??
)??
C.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
D.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】盒中共有形狀大小完全相同的5個球,其中有2個紅球和3個白球.若從中隨機(jī)取2個球,則概率為 ![]() 的事件是( )
的事件是( )
A.都不是紅球
B.恰有1個紅球
C.至少有1個紅球
D.至多有1個紅球
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,以極點(diǎn)為原點(diǎn),極軸為
,以極點(diǎn)為原點(diǎn),極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系,直線
軸的正半軸建立平面直角坐標(biāo)系,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).
為參數(shù)).
(I)寫出直線![]() 的一般方程與曲線
的一般方程與曲線![]() 的直角坐標(biāo)方程,并判斷它們的位置關(guān)系;
的直角坐標(biāo)方程,并判斷它們的位置關(guān)系;
(II)將曲線![]() 向左平移
向左平移![]() 個單位長度,向上平移
個單位長度,向上平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]() ,設(shè)曲線
,設(shè)曲線![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換![]() 得到曲線
得到曲線![]() ,設(shè)曲線
,設(shè)曲線![]() 上任一點(diǎn)為
上任一點(diǎn)為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定義域和值域均是[1,a],求實(shí)數(shù)a的值;
(2)若對任意的x1 , x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,AB=4,BC=3,點(diǎn)D在線段AC上,且AD=4DC. 
(Ⅰ)求BD的長;
(Ⅱ)求sin∠CBD的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com