Question

已知中心在原點，焦點在x軸上的雙曲線的一條漸近線為mx-y=0，若m在集合{1，2，3，4，5，6，7，8，9}中任意取一個值，使得雙曲線的離心率大于3的概率是     ．

Answer 1

【答案】分析：由題意可得屬于古典概率模型，由古典概率的計算公式，分別計算試驗的結果n，基本事件的結果m，代入古典概率的計算公式P=．
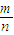
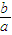
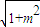
解答：解析：由題意知m=，e=，當m=1或2時，1＜e＜3
若m在集合{1，2，3，4，5，6，7，8，9}中任意取一個值的結果有9種結果，記“使得雙曲線的離心率大于3”為事件A，則A包含的結果有3，4，5，6，7，8，9共7中結果
由古典概率的計算公式可得：P（A）=．
答案：
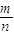
點評：本題主要考查了古典概率的計算公式P=，求解的關鍵是要確定試驗的所有結果數n及基本事件的個數m，屬于對基本知識的簡單運用的考查，試題較易．