【題目】
已知f（x）=lnx+a（1-x）,問:（1）討論f（x） 的單調性；（2）當 f（x）有最大值,且最大值大于2a-2 時,求a的取值范圍.
（1）（I）討論f（x） 的單調性；
（2）（II）當 f（x）有最大值,且最大值大于2a-2 時,求a的取值范圍.
【答案】
（1）
f（x）在（0，
）單調遞增，在（，+
）單調遞減
（2）
（0,1）
【解析】
（I)a
0，f（x）在（0，+）是單調遞增
a
0.f（x）在（0，）單調遞增，在（ ， +）單調遞減
f（x）的定義域為（0，+），f’（x）=
-a,若a0，則f’（x）0，f（x）在（0，+）是單調遞增
若a0，則當x
（0，）時，f’（x）0，
當x（ ， +）時，f’（x）
0
所以f（x）在（0，）單調遞增，在（ ， +）單調遞減。
(II).由（I）知，當a
0時，f（x）在（0，+）無最大值
當a0.f（x）在x=取得最大值，最大值為f（）=ln（）+a（1-）=-lna+a-1
因此f（）2a-2
lna+a-10
令g（a）=lna+a-1，則g（a）在（0，+）是增函數，g（1）=0，于是，當0a1時g（a）0，當a1時，g（a）0，因此a的取值范圍是（0,1）。
【考點精析】通過靈活運用函數單調性的判斷方法，掌握單調性的判定法：①設x1,x2是所研究區間內任兩個自變量，且x1＜x2；②判定f(x1)與f(x2)的大小；③作差比較或作商比較即可以解答此題．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，已知菱形ABEF所在的平面與△ABC所在的平面相互垂直，AB=4，BC= 
，BC⊥BE，∠ABE= 
．
（1）求證：BC⊥平面ABEF；
（2）求平面ACF與平面BCE所成的銳二面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知D= 
，給出下列四個命題：
P1：（x，y）∈D，x+y+1≥0；
P2：（x，y）∈D，2x﹣y+2≤0；
P3：（x，y）∈D， 
≤﹣4；
P4：（x，y）∈D，x2+y2≤2．
其中真命題的是（ ）
A.P1 ， P2
B.P2 ， P3
C.P2 ， P4
D.P3 ， P4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a，b，c分別是△ABC的內角A，B，C所對的邊，a=2bcosB，b≠c．
（1）證明：A=2B；
（2）若a2+c2=b2+2acsinC，求A．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
如圖，長方形的邊AB=2，BC=1，O是AB的中點，點P沿著邊BC，CD與DA運動，記
BOP=x，將動點P到A,B兩點距離之和表示為x的函數f（x），則圖像大致為（）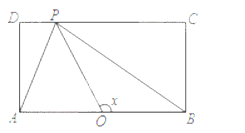
A.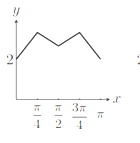
B.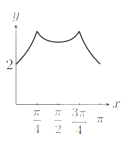
C.
D.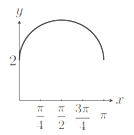
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
如圖，長方形的邊AB=2，BC=1，O是AB的中點，點P沿著邊BC，CD與DA運動，記
BOP=x，將動點P到A,B兩點距離之和表示為x的函數f（x），則圖像大致為（）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖O是等腰三角形ABC內一點,圓O與△ABC的底邊BC交于M,N兩點,與底邊上的高交于點G,且與AB,AC分別相切于E,F兩點.
（1）(I)證明EF//BC
（2）(II)若AG等于圓O半徑，且AE=MN=2
，求四邊形EBCF的面積
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2015·新課標I卷）Sn為數列{an}的前n項和.已知an＞0，an2+2an=4Sn+3,
（1）求{an}的通項公式；
（2）設bn=
,求數列{bn}的前n項和.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項的和記為Sn．如果a4＝－12，a8＝－4．
(1)求數列{an}的通項公式；
(2)求Sn的最小值及其相應的n的值；
(3)從數列{an}中依次取出a1，a2，a4，a8，…，
，…，構成一個新的數列{bn}，求{bn}的前n項和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com