
(本小題滿分12分)已知函數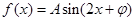
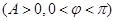 ,當
,當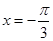 時取得最小值-4.
時取得最小值-4.
(1)求函數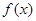 的解析式;
的解析式;
(2)若等差數列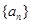 前n項和為
前n項和為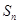 ,且
,且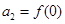 ,
, ,求數列
,求數列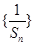 的前n項和
的前n項和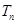 .
.
(1) ;(2)
;(2) .
.
解析試題分析: 本題是三角函數與數列的綜合題目,考查三角函數的最值、解析式,數列的通項公式、求和公式等基礎知識,考查數形結合思想、轉化思想和計算能力.第一問,根據已知條件,當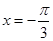 時取得最小值-4,所以數形結合將坐標代入解出
時取得最小值-4,所以數形結合將坐標代入解出 的值,得到函數解析式;第二問,根據第一問的解析式,先求出
的值,得到函數解析式;第二問,根據第一問的解析式,先求出 和
和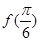 即
即 和
和 的值,利用等差數列的通項公式求出數列
的值,利用等差數列的通項公式求出數列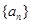 的首項和公差,并求出數列的前n項和
的首項和公差,并求出數列的前n項和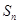 ,用裂項相消法求數列
,用裂項相消法求數列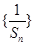 的前n項和.
的前n項和.
試題解析:(1)由題意 時取得最小值-4,
時取得最小值-4, ,
,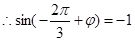 ,
,
又因為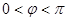 ,
,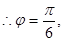 所以
所以 4分
4分
(2)因為 ,
, ,所以
,所以 ,
,
設等差數列公差為 ,則
,則 ,
, 8分
8分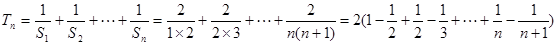
 12分
12分
考點:1.三角函數的最值;2.等差數列的通項公式;3.等差數列的前n項和公式;4.裂項相消法求和.


科目:高中數學 來源: 題型:解答題
中國人口已經出現老齡化與少子化并存的結構特征,測算顯示中國是世界上人口老齡化速度最快的國家之一,再不實施“放開二胎”新政策,整個社會將會出現一系列的問題.若某地區2012年人口總數為45萬,實施“放開二胎”新政策后專家估計人口總數將發生如下變化:從2013年開始到2022年每年人口比上年增加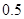 萬人,從2023年開始到2032年每年人口為上一年的99%.
萬人,從2023年開始到2032年每年人口為上一年的99%.
(1)求實施新政策后第 年的人口總數
年的人口總數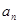 的表達式(注:2013年為第一年);
的表達式(注:2013年為第一年);
(2)若新政策實施后的2013年到2032年人口平均值超過49萬,則需調整政策,否則繼續實施.問到2032年后是否需要調整政策?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設等差數列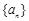 的前
的前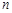 項和為
項和為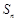 ,已知
,已知 ,
,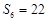 .
.
(1)求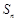 ;
;
(2)若從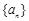 中抽取一個公比為
中抽取一個公比為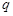 的等比數列
的等比數列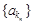 ,其中
,其中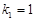 ,且
,且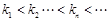 ,
,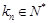 .
.
①當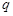 取最小值時,求
取最小值時,求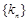 的通項公式;
的通項公式;
②若關于 的不等式
的不等式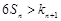 有解,試求
有解,試求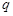 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列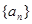 滿足
滿足 (
( ).
).
(1)若數列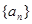 是等差數列,求它的首項和公差;
是等差數列,求它的首項和公差;
(2)證明:數列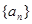 不可能是等比數列;
不可能是等比數列;
(3)若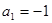 ,
, (
( ),試求實數
),試求實數 和
和 的值,使得數列
的值,使得數列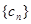 為等比數列;并求此時數列
為等比數列;并求此時數列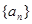 的通項公式.
的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com