
【題目】已知函數f(x)= ![]() sinx+cosωx(ω>0)的圖象與x軸交點的橫坐標依次構成一個公差為
sinx+cosωx(ω>0)的圖象與x軸交點的橫坐標依次構成一個公差為 ![]() 的等差數列,把函數f(x)的圖象沿x軸向左平移
的等差數列,把函數f(x)的圖象沿x軸向左平移 ![]() 個單位,得到函數g(x)的圖象,則( )
個單位,得到函數g(x)的圖象,則( )
A.g(x)是奇函數
B.g(x)關于直線x=﹣ ![]() 對稱
對稱
C.g(x)在[ ![]() ,
, ![]() ]上是增函數
]上是增函數
D.當x∈[ ![]() ,
, ![]() ]時,g(x)的值域是[2,1]
]時,g(x)的值域是[2,1]
【答案】D
【解析】解:f(x)= ![]() sinx+cosωx(ω>0),
sinx+cosωx(ω>0),
化簡得:f(x)=2sin(x+ ![]() ),
),
∵圖象與x軸交點的橫坐標依次構成一個公差為 ![]() 的等差數列,可知周期為π
的等差數列,可知周期為π
∴T=π= ![]() ,解得ω=2.
,解得ω=2.
那么:f(x)=2sin(2x+ ![]() ),圖象沿x軸向左平移
),圖象沿x軸向左平移 ![]() 個單位,得:2sin[2(x+
個單位,得:2sin[2(x+ ![]() )+
)+ ![]() ]=2cos2x.
]=2cos2x.
∴g(x)=2cos2x,故g(x)是偶函數,在區間[0, ![]() ]單調減函數.所以A,C不對.
]單調減函數.所以A,C不對.
對稱軸方程為x= ![]() (k=Z),檢驗B不對.
(k=Z),檢驗B不對.
當x∈[ ![]() ,
, ![]() ]時,那么2x∈[
]時,那么2x∈[ ![]() ,
, ![]() ],g(x)的最大值為1,最小值為﹣2,故值域為[﹣2,1].D正確.
],g(x)的最大值為1,最小值為﹣2,故值域為[﹣2,1].D正確.
故選:D.
【考點精析】解答此題的關鍵在于理解函數y=Asin(ωx+φ)的圖象變換的相關知識,掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,當x≥0時,f(x)=x2–2x+2.
(1)求函數f(x)的解析式;
(2)當x∈[m,n]時,f(x)的取值范圍為[2m,2n],試求實數m,n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某市![]() 年
年![]() 月
月![]() 日至
日至![]() 日的空氣質量指數趨勢圖,某人隨機選擇
日的空氣質量指數趨勢圖,某人隨機選擇![]() 年
年![]() 月
月![]() 日至
日至![]() 月
月![]() 日中的某一天到達該市,并停留
日中的某一天到達該市,并停留![]() 天.
天.

(1)求此人到達當日空氣質量指數大于![]() 的概率;
的概率;
(2)設![]() 是此人停留期間空氣質量指數小于
是此人停留期間空氣質量指數小于![]() 的天數,求
的天數,求![]() 的分布列與數學期望;
的分布列與數學期望;
(3)由圖判斷從哪天開始連續三天的空氣質量指數方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD-A′B′C′D′的棱長為a,連接A′C′,A′D,A′B,BD,BC′,C′D,得到一個三棱錐.求:
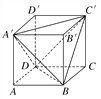
(1)三棱錐A′-BC′D的表面積與正方體表面積的比值;
(2)三棱錐A′-BC′D的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區有1500戶居民,其中平原地區1050戶,山區450戶,為調查該地區2017年家庭收入情況,從而更好地實施“精準扶貧”,采用分層抽樣的方法,收集了150戶家庭2017年年收入的樣本數據(單位:萬元)
(I)應收集多少戶山區家庭的樣本數據?
(Ⅱ)根據這150個樣本數據,得到2017年家庭收入的頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果將頻率率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
.如果將頻率率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
(Ⅲ)樣本數據中,由5戶山區家庭的年收入超過2萬元,請完成2017年家庭收入與地區的列聯表,并判斷是否有90%的把握認為“該地區2017年家庭年收入與地區有關”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超過2萬元 | 不超過2萬元 | 總計 | |
平原地區 | |||
山區 | 5 | ||
總計 |

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一張坐標紙上已作出圓![]() 及點
及點![]() ,折疊此紙片,使
,折疊此紙片,使![]() 與圓周上某點
與圓周上某點![]() 重合,每次折疊都會留下折痕,設折痕與直線
重合,每次折疊都會留下折痕,設折痕與直線![]() 的交點為
的交點為![]() ,令點
,令點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.

(1)求曲線![]() 的方程;
的方程;
(2)若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 、
、![]() 兩點,且直線
兩點,且直線![]() 與以
與以![]() 為直徑的圓相切,若
為直徑的圓相切,若![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象過點
的圖象過點![]() .
.
(1)求![]() 的值并求函數
的值并求函數![]() 的值域;
的值域;
(2)若關于![]() 的方程
的方程![]() 有實根,求實數
有實根,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,則是否存在實數
,則是否存在實數![]() ,使得函數
,使得函數![]() 的最大值為
的最大值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小張經營某一消費品專賣店,已知該消費品的進價為每件40元,該店每月銷售量(百件)與銷售單價x(元/件)之間的關系用下圖的一折線表示,職工每人每月工資為1000元,該店還應交付的其它費用為每月10000元.

(1)把y表示為x的函數;
(2)當銷售價為每件50元時,該店正好收支平衡(即利潤為零),求該店的職工人數;
(3)若該店只有20名職工,問銷售單價定為多少元時,該專賣店可獲得最大月利潤?(注:利潤=收入-支出)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com