
【題目】設等差數列![]() 滿足
滿足![]() ,
,![]() ,
,
(1)求數列![]() 的通項公式;
的通項公式;
(2)求![]() 的最大項的值;
的最大項的值;
(3)數列![]() 滿足
滿足![]() ,問是否存在正整數k,使得
,問是否存在正整數k,使得![]()
![]() 成等差數列?若存在,求出k和m的值;若不存在,請說明理由.
成等差數列?若存在,求出k和m的值;若不存在,請說明理由.
【答案】(1)![]() (2)最大項的值為1(3)不存在,詳見解析
(2)最大項的值為1(3)不存在,詳見解析
【解析】
(1)根據題意,設等差數列{an}的公差為d,首項為a1,由條件列得方程組,解可得d與a1,由等差數列通項公式可得答案;
(2)直接利用![]() 的單調性,即可得出.
的單調性,即可得出.
(3)結合(1)知![]() .要使b1,b2,bm成等差數列,可得2b2=b1+bm,代入化簡運算即可得出.
.要使b1,b2,bm成等差數列,可得2b2=b1+bm,代入化簡運算即可得出.
(1)設等差數列的首項為![]() ,公差為d,
,公差為d,
由題意得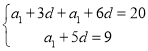 ,解得
,解得![]() ,
,
數列![]() 的通項公式
的通項公式![]() ;
;
(2)令![]() ,
,
當![]() 時,
時,![]() 且隨n的增大而增大,即有
且隨n的增大而增大,即有![]() ;當
;當![]() 時,
時,![]() ;
;
所以![]() 的最大項的值為1;
的最大項的值為1;
(3)假設存在正整數![]() ,使得
,使得![]()
![]() 成等差數列,
成等差數列,
由![]() 得
得![]() ,從而
,從而![]() ,
,![]() ,由
,由![]() 得,
得,![]() ,
,
所以![]() ,兩邊取倒數整理得:
,兩邊取倒數整理得:![]() ,
,
所以![]() ,即
,即![]() ,
,
因為k、m均為正整數,
所以![]() ,不能得出
,不能得出![]() 為整數,故無符合題意的解,
為整數,故無符合題意的解,
所以不存在正整數k,使得![]()
![]() 成等差數列.
成等差數列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,其前n項和為Sn , {bn}是等比數列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求數列{an}與{bn}的通項公式;
(2)記Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 證明:Tn+12=﹣2an+10bn(n∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體 ABCD-A1B1C1D1 的棱長為 1 , E 、F 分別是棱 AB 、BC上的動點 ,且AE = BF .求直線 A1E 與C1F 所成角的最小值(用反三角函數表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,點
,點![]() 是橢圓上的一個動點,
是橢圓上的一個動點,![]() 面積的最大值是
面積的最大值是![]() .
.
(1)求橢圓的方程;
(2)若![]() 是橢圓上不重合的四點,
是橢圓上不重合的四點,![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,且
,且![]() ,求此時直線
,求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場預測,投資債券等穩(wěn)健型產品的收益![]() 與投資額
與投資額![]() 成正比,且投資1萬元時的收益為
成正比,且投資1萬元時的收益為![]() 萬元,投資股票等風險型產品的收益
萬元,投資股票等風險型產品的收益![]() 與投資額
與投資額![]() 的算術平方根成正比,且投資1萬元時的收益為0.5萬元,
的算術平方根成正比,且投資1萬元時的收益為0.5萬元,
(1)分別寫出兩種產品的收益與投資額的函數關系;
(2)該家庭現有20萬元資金,全部用于理財投資,問:怎樣分配資金能使投資獲得最大收益,其最大收益為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,點
,點![]() 是圓
是圓![]() 上的一個動點,點
上的一個動點,點![]()
![]() 分別在線段
分別在線段![]()
![]() 上,且滿足
上,且滿足![]() ,
,![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與點
與點![]() 的軌跡相交于
的軌跡相交于![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形?如果存在,求出
為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,說明理由.
的取值范圍;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值來衡量,質量指標值越大表明質量越好,記其質量指標值為![]() ,當
,當![]() 時,產品為一級品;當
時,產品為一級品;當![]() 時,產品為二級品,當
時,產品為二級品,當![]() 時,產品為三級品,現用兩種新配方(分別稱為
時,產品為三級品,現用兩種新配方(分別稱為![]() 配方和
配方和![]() 配方)做實驗,各生產了
配方)做實驗,各生產了![]() 件這種產品,并測量了每件產品的質量指標值,得到下面的試驗結果 :(以下均視頻率為概率)
件這種產品,并測量了每件產品的質量指標值,得到下面的試驗結果 :(以下均視頻率為概率)
![]() 配方的頻數分配表:
配方的頻數分配表:
指標值分組 |
|
|
|
|
頻數 |
|
|
|
|
![]() 配方的頻數分配表:
配方的頻數分配表:
指標值分組 |
|
|
|
|
|
頻數 |
|
|
|
|
|
(1)若從![]() 配方產品中有放回地隨機抽取
配方產品中有放回地隨機抽取![]() 件,記“抽出的
件,記“抽出的![]() 配方產品中至少
配方產品中至少![]() 件二級品”為事件
件二級品”為事件![]() ,求事件
,求事件![]() 發(fā)生的概率
發(fā)生的概率![]() ;
;
(2)若兩種新產品的利潤率![]() 與質量指標
與質量指標![]() 滿足如下關系:
滿足如下關系: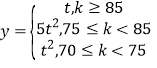 ,其中
,其中![]() ,從長期來看,投資哪種配方的產品平均利潤率較大?
,從長期來看,投資哪種配方的產品平均利潤率較大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com