
【題目】已知橢圓![]() ,與
,與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,右焦點
,右焦點![]() ,
, ![]() 為坐標原點,且
為坐標原點,且![]() .
.
(1)求橢圓的離心率![]() ;
;
(2)已知點![]() ,過點
,過點![]() 任意作直線
任意作直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,設直線
兩點,設直線![]() 的斜率
的斜率![]() ,若
,若![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)tan∠PFO=![]() 可得
可得![]() =
=![]() ,c=
,c=![]() b,a=
b,a=![]() =
=![]() b即可得出(2)直線斜率不為0時,設出直線方程ty=x﹣1,設C(x1,y1),D(x2,y2).聯立
b即可得出(2)直線斜率不為0時,設出直線方程ty=x﹣1,設C(x1,y1),D(x2,y2).聯立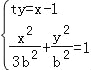 ,化為:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴
,化為:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴![]() +
+![]() =2,根據韋達定理代入求解即可,斜率為0 時也成立
=2,根據韋達定理代入求解即可,斜率為0 時也成立
試題解析:
(1)∵tan∠PFO=![]() ,∴
,∴![]() =
=![]() ,∴c=
,∴c=![]() b,a=
b,a=![]() =
=![]() b.
b.
∴![]() =
=![]() =
=![]() .
.
(2)直線l的斜率不為0時,設直線l的方程為:ty=x﹣1.設C(x1,y1),D(x2,y2).
聯立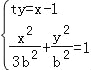 ,化為:(t2+3)y2+2ty+1﹣3b2=0,
,化為:(t2+3)y2+2ty+1﹣3b2=0,
y1+y2=![]() ,y1y2=
,y1y2=![]() ,
,
∵k1+k2=2,∴![]() +
+![]() =2,
=2,
化為:(y1﹣2)(ty2﹣2)+(y2﹣2)(ty1﹣2)=2(ty1﹣2)(ty2﹣2),
即:ty1y2=y1+y2,
∴t![]() =
=![]() ,對t∈R都成立.
,對t∈R都成立.
化為:b2=1,
直線l的斜率為0時也成立,
∴b2=1,
∴橢圓C的方程為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() 在
在![]() 和
和![]() 處取得極值,且
處取得極值,且![]() ,曲線
,曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)證明關于![]() 的方程
的方程![]() 至多只有兩個實數根(其中
至多只有兩個實數根(其中![]() 是
是![]() 的導函數,
的導函數, ![]() 是自然對數的底數).
是自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m個正數a1 , a2 , …,am(m≥4,m∈N*)依次圍成一個圓圈.其中a1 , a2 , a3 , …ak﹣1 , ak(k<m,k∈N*)是公差為d的等差數列,而a1 , am , am﹣1 , …,ak+1 , ak是公比為2的等比數列.
(1)若a1=d=2,k=8,求數列a1 , a2 , …,am的所有項的和Sm;
(2)若a1=d=2,m<2015,求m的最大值;
(3)是否存在正整數k,滿足a1+a2+…+ak﹣1+ak=3(ak+1+ak+2+…+am﹣1+am)?若存在,求出k值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】互不相等的三個正數x1 , x2 , x3成等比數列,且點P1(logax1 , logby1)P2(logax2 , logby2),P3(logax3 , logby3)共線(a>0且a≠0,b>且b≠1)則y1 , y2 , y3成( )
A.等差數列,但不等比數列
B.等比數列而非等差數列
C.等比數列,也可能成等差數列
D.既不是等比數列,又不是等差數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,小明想將短軸長為2,長軸長為4的一個半橢圓形紙片剪成等腰梯形ABDE,且梯形ABDE內接于半橢圓,DE∥AB,AB為短軸,OC為長半軸
(1)求梯形ABDE上底邊DE與高OH長的關系式;
(2)若半橢圓上到H的距離最小的點恰好為C點,求底邊DE的取值范圍

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對創“市級示范性學校”的甲、乙兩所學校進行復查驗收,對辦學的社會滿意度一項評價隨機訪問了20為市民,這20位市民對這兩所學校的評分(評分越高表明市民的評價越好)的數據如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
檢查組將成績分成了四個等級:成績在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 為
為![]() 等.
等.
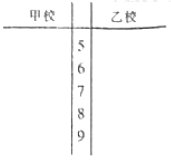
(1)請用莖葉圖表示上面的數據,并通過觀察莖葉圖,對兩所學校辦學的社會滿意度進行比較,寫出兩個統計結論;
(2)根據所給數據,以事件發生的頻率作為相應事件發生的概率,求乙校得分的等級高于甲校得分的等級的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com