
【題目】已知△ABC中,角A,B,C所對的邊分別為a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1﹣cosC). 
(1)判斷△ABC的形狀;
(2)在△ABC的邊AB,AC上分別取D,E兩點,使沿線段DE折疊三角形時,頂點A正好落在邊BC上的P點處,設∠BDP=θ,當AD最小時,求 ![]() 的值.
的值.
【答案】
(1)解:由sin2A+sin2B=sin2C+sinAsinB得a2+b2=c2+ab
∴ ![]()
又0<C<π∴ ![]()
又由 ccosB=b(1﹣cosC)得:sinCcosB=sinB(1﹣cosC)
∴sinCcosB+sinBcosC=sinB∴sin(B+C)=sinB
即sinA=sinB∴a=b
故△ABC為等邊三角形
(2)解:如圖:連結AP,

∵AD=DP∴θ=2∠BAP
∴ ![]()
又設AD=DP=y,AB=a,則BD=a﹣y
在△BDP中,由正弦定理有: ![]()
∴ ![]()
故 
![]()
∴ ![]() 時
時 ![]()
此時 ![]()
【解析】(1)利用正弦定理以及余弦定理,結合兩角和與差的三角函數,判斷三角形的形狀.(2)連結AP,設AD=DP=y,AB=a,則BD=a﹣y,由正弦定理求出表達式,通過三角函數的最值求解就.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是
是![]() 的中點,底面
的中點,底面![]() 為矩形,
為矩形, ![]() ,
, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 與棱
與棱![]() 交于點
交于點![]() ,平面
,平面![]() 與平面
與平面![]() 交于直線
交于直線![]() .
.
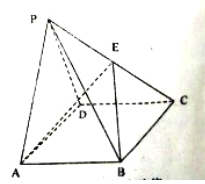
(1)求證: ![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)求與直線3x+4y-7=0垂直,且與原點的距離為6的直線方程;
(2)求經過直線l1:2x+3y-5=0與l2:7x+15y+1=0的交點,且平行于直線x+2y-3=0的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)寫出曲線![]() 的參數方程和直線
的參數方程和直線![]() 的普通方程;
的普通方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,求點
上一點,求點![]() 到直線
到直線![]() 的最小距離.
的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠隨機抽取部分工人調查其上班路上所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),若上班路上所需時間的范圍是[0,100],樣本數據分組為[0,20),[20,40),[40,60),[60,80),[80,100]. 
(1)求直方圖中a的值;
(2)如果上班路上所需時間不少于1小時的工人可申請在工廠住宿,若招工2400人,請估計所招工人中有多少名工人可以申請住宿;
(3)該工廠工人上班路上所需的平均時間大約是多少分鐘.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C: ![]() (a>0,b>0)過點A(1,0),且離心率為
(a>0,b>0)過點A(1,0),且離心率為 ![]()
(1)求雙曲線C的方程;
(2)已知直線x﹣y+m=0與雙曲線C交于不同的兩點A,B,且線段AB的中點在圓x2+y2=5上,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com