
【題目】一幾何體按比例繪制的三視圖如圖所示:
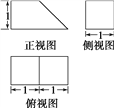
(1)試畫出它的直觀圖;
(2)求它的表面積和體積.
【答案】(1)見解析;(2)表面積為![]() ,體積為
,體積為![]()
【解析】試題分析:(1)由三視圖畫出它的直觀圖;(2)該幾何體是長方體被截去一個三棱柱,且該幾何體的體積是以A1A,A1D1,A1B1為棱的長方體的體積的![]() .
.
試題解析:
(1)直觀圖如圖所示.
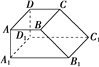
(2)由三視圖可知該幾何體是長方體被截去一個三棱柱,且該幾何體的體積是以A1A,A1D1,A1B1為棱的長方體的體積的![]() ,在直角梯形AA1B1B中,作BE⊥A1B1于E,
,在直角梯形AA1B1B中,作BE⊥A1B1于E,
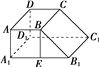
則四邊形AA1EB是正方形,AA1=BE=1,
在Rt△BEB1中,BE=1,EB1=1,所以BB1=![]() ,
,
所以幾何體的表面積
S=S正方形ABCD+S矩形A1B1C1D1+2S梯形AA1B1B+S矩形BB1C1C+S正方形AA1D1D
=1+2×1+2×![]() ×(1+2)×1+1×
×(1+2)×1+1×![]() +1=(7+
+1=(7+![]() ).
).
幾何體的體積V=![]() ×1×2×1=
×1×2×1=![]() .
.
所以該幾何體的表面積為(7+![]() ),體積為
),體積為![]()


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】寧德被譽為“中國大黃魚之鄉”,海域面積4.46萬平方公里,水產資源極為豐富.“寧德大黃魚”作為福建寧德地理標志產品,同時也是寧德最具區域特色的海水養殖品種,全國80%以上的大黃魚產自寧德,年產值超過60億元.現有一養殖戶為了解大黃魚的生長狀況,對其漁場中100萬尾魚的凈重(單位:克)進行抽樣檢測,將抽樣所得數據繪制成頻率分布直方圖如圖.其中產品凈重的范圍是![]() ,已知樣本中產 品凈重小于100克的有360尾.
,已知樣本中產 品凈重小于100克的有360尾.

(1)計算樣本中大黃魚的數量;
(2)假設樣本平均值不低于101.3克的漁場為![]() 級漁場,否則為
級漁場,否則為![]() 級漁場.那么要使得該漁場為
級漁場.那么要使得該漁場為![]() 級漁場,則樣本中凈重在
級漁場,則樣本中凈重在![]() 的大黃魚最多有幾尾?
的大黃魚最多有幾尾?
(3)為提升養殖效果,該養殖戶進行低沉性配合飼料養殖,凈重小于98克的每4萬尾合用一個網箱,大于等于98克的每3萬尾合用一個網箱.根據(2)中所求的最大值,估計該養殖戶需要準備多少個網箱?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,空氣質量成為人們越來越關注的話題,空氣質量指數(,Air Quality Inder簡稱 ![]() )是定量描述空氣質量狀況的指數,空氣質量按照
)是定量描述空氣質量狀況的指數,空氣質量按照 ![]() 大小分為六級,
大小分為六級, ![]() 為優;
為優; ![]() 為良;
為良; ![]() 為輕度污染;
為輕度污染; ![]() 為中度污染;
為中度污染; ![]() 為重度污染;大于300為嚴重污染.環保部門記錄了2017年某月哈爾濱市10天的
為重度污染;大于300為嚴重污染.環保部門記錄了2017年某月哈爾濱市10天的 ![]() 的莖葉圖如下:
的莖葉圖如下: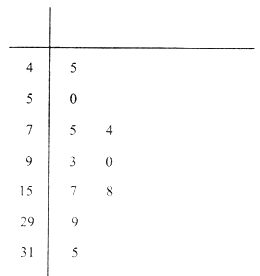
(1)利用該樣本估計該地本月空氣質量優良( ![]() )的天數;(按這個月總共30天計算)
)的天數;(按這個月總共30天計算)
(2)現工作人員從這10天中空氣質量為優良的日子里隨機抽取2天進行某項研究,求抽取的2天中至少有一天空氣質量是優的概率;
(3)將頻率視為概率,從本月中隨機抽取3天,記空氣質量優良的天數為 ![]() ,求
,求 ![]() 的概率分布列和數學期望.
的概率分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
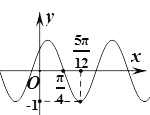
【題目】函數![]() (其中
(其中![]() )的部分圖象如圖所示,為了得到
)的部分圖象如圖所示,為了得到![]() 的圖象,只要將
的圖象,只要將![]() 的圖象
的圖象
A. 先向右平移![]() 個單位長度,再把所得各點的橫坐標伸長到原來的
個單位長度,再把所得各點的橫坐標伸長到原來的![]() 倍,縱坐標不變
倍,縱坐標不變
B. 先向右平移![]() 個單位長度,再把所得各點的橫坐標伸長到原來的
個單位長度,再把所得各點的橫坐標伸長到原來的![]() 倍,縱坐標不變
倍,縱坐標不變
C. 先向左平移![]() 個單位長度 ,再把所得各點的橫坐標縮短到原來的
個單位長度 ,再把所得各點的橫坐標縮短到原來的![]() 倍,縱坐標不變
倍,縱坐標不變
D. 先向左平移![]() 個單位長度, 再把所得各點的橫坐標縮短到原來的
個單位長度, 再把所得各點的橫坐標縮短到原來的![]() 倍,縱坐標不變
倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ax2+2(a﹣3)x+1在區間[﹣2,+∞)上遞減,則實數a的取值范圍是( )
A.(﹣∞,0)
B.[﹣3,+∞)
C.[﹣3,0]
D.(0,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個結論: ①若x>0,則x>sinx恒成立;
②“若am2<bm2 , 則a<b”的逆命題為真命題
③m∈R,使f(x)=(m﹣1)x ![]() 是冪函數,且在(﹣∞,0)上單調遞減
是冪函數,且在(﹣∞,0)上單調遞減
④對于命題p:x∈R使得x2+x+1<0,則¬p:x∈R,均有x2+x+1>0
其中正確結論的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com