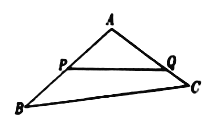
【題目】如圖，某生態園將一塊三角形地
的一角
開辟為水果園，已知角
為
， 
的長度均大于200米，現在邊界
處建圍墻，在
處圍竹籬笆.
（1）若圍墻
、
總長度為200米，如何可使得三角形地塊
面積最大？
（2）已知竹籬笆長為
米， 
段圍墻高1米， 
段圍墻高2米，造價均為每平方米100元，若
，求圍墻總造價的取值范圍.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知圓
經過點
， 
，并且直線
平分圓.
（1）求圓的方程；
（2）若直線
與圓交于
兩點，是否存在直線
，使得
（
為坐標原點），若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2﹣lnx．
（1）求曲線f（x）在點（1，f（1））處的切線方程；
（2）求函數f（x）的單調遞減區間：
（3）設函數g（x）=f（x）﹣x2+ax，a＞0，若x∈（O，e]時，g（x）的最小值是3，求實數a的值．（e為自然對數的底數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是公差為2的等差數列，且a1 ， a4 ， a13成等比數列，數列{ 
}是首項為1，公比為3的等比數列．
（1）求數列{an}、{bn}的通項公式；
（2）設數列{an+bn}的前n項和Rn ， 若不等式 
≤λ3n+n+3對n∈N*恒成立，求λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
是等邊三角形，邊長為4， 
邊的中點為
，橢圓
以
， 
為左、右兩焦點，且經過
、
兩點。
（1）求該橢圓的標準方程；
（2）過點
且
軸不垂直的直線
交橢圓于
， 
兩點，求證：直線
與
的交點在一條定直線上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
的極坐標方程是
，以極點為原點，極軸為
軸的正半軸建立平面直角坐標系，直線
的參數方程為
（
為參數）.
（Ⅰ）寫出直線
的普通方程與曲線
的直角坐標方程；
（Ⅱ）設曲線
經過伸縮變換
得到曲線
，若點
，直線
與
交與
， 
，求
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2＋y2＋2x－4y＋3＝0．
(1)若圓C的切線在x軸和y軸上的截距相等，求此切線的方程．
(2)從圓C外一點P(x1，y1)向該圓引一條切線，切點為M，O為坐標原點，且有|PM|＝|PO|，求使得|PM|取得最小值的點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
