
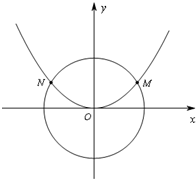
如圖,已知拋物線C1:x2=2py(p>0)與圓C2:x2+y2=![]() 交于M、N兩點,且∠MON=120°.
交于M、N兩點,且∠MON=120°.
(1)求拋物線C1的方程;
(2)設直線l與圓C2相切.
①若直線l與拋物線C1也相切,求直線l的方程.
②若直線l與拋物線C1交于不同的A、B兩點,求![]() ·
·![]() 的取值范圍.
的取值范圍.
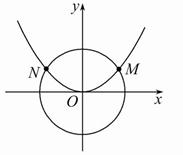
(1)因為∠MON=120°,所以OM與x軸正半軸成30°角,所以點M的坐標為(![]() ,
,![]() ),代入拋物線方程得(
),代入拋物線方程得(![]() )2=2p×
)2=2p×![]() ,求得p=1,
,求得p=1,
所以拋物線C1的方程為x2=2y.
(2)由題意可設l:y=kx+b,即kx-y+b=0,
因為l與圓C2相切,所以![]() =
=![]() ,
,
即9b2=16(k2+1) (Ⅰ)
①設直線l與拋物線C1:x2=2y即y=![]() x2相切于點T(t,
x2相切于點T(t,![]() t2),因為函數y=
t2),因為函數y=![]() x2的導數為y′=x,所以
x2的導數為y′=x,所以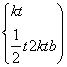 (Ⅱ)
(Ⅱ)
由(Ⅰ)、(Ⅱ)解得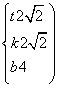 或
或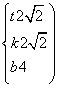
所以直線l的方程為y=-2![]() x-4或y=2
x-4或y=2![]() x-4.
x-4.
②由![]() 得x2-2kx
得x2-2kx![]() -2b=0,
-2b=0,
設A(x1,y1),B(x2,y2),
則x1+x2=2k,x1x2=-2b,且由Δ=4k2+8b>0得k2+2b>0 (Ⅲ)
由(Ⅰ)、(Ⅲ)可得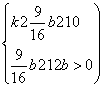 ,解得b≥
,解得b≥![]() 或b<-4,
或b<-4,
所以![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() (x1x2)2+x1x2=b2-2b∈[-
(x1x2)2+x1x2=b2-2b∈[-![]() ,+∞),即
,+∞),即![]() ·
·![]() 的取值范圍是[-
的取值范圍是[-![]() ,+∞).
,+∞).


 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源: 題型:
 (2013•嘉興二模)如圖,已知拋物線C1:x2=2py的焦點在拋物線C2:y=
(2013•嘉興二模)如圖,已知拋物線C1:x2=2py的焦點在拋物線C2:y=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•嘉興二模)如圖,已知拋物線C1:x2=2py的焦點在拋物線C2:y=
(2013•嘉興二模)如圖,已知拋物線C1:x2=2py的焦點在拋物線C2:y=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知拋物線C1:x2=2py(p>0)與圓C2:x2+y2=
如圖,已知拋物線C1:x2=2py(p>0)與圓C2:x2+y2=| 16 |
| 9 |
| OA |
| OB |
查看答案和解析>>
科目:高中數學 來源:2014屆江西吉安二中高二月考文科數學試卷(解析版) 題型:解答題
(14分)如圖,已知拋物線C1: y=x2, 與圓C2: x2+(y+1)2="1," 過y軸上一點A(0, a)(a>0)作圓C2的切線AD,切點為D(x0, y0).

(1)證明:(a+1)(y0+1)=1
(2)若切線AD交拋物線C1于E,且E為AD的中點,求點A縱坐標a.
查看答案和解析>>
科目:高中數學 來源:2011年福建省南平市高三適應性考試數學試卷(理科)(解析版) 題型:解答題
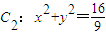 交于M、N兩點,
交于M、N兩點,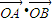 的取值范圍.
的取值范圍.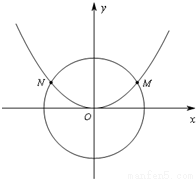
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com