
【題目】已知函數![]() (
(![]() ,
,![]() 為自然對數的底數).
為自然對數的底數).
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 有兩個極值點,求實數
有兩個極值點,求實數![]() 的取值范圍;
的取值范圍;
【答案】(1)![]() 單調遞增區間是
單調遞增區間是![]() ,無單調遞減區間;(2)
,無單調遞減區間;(2)![]() .
.
【解析】
(1)求出![]() ,由已知可得
,由已知可得![]() ,進而求出
,進而求出![]() ,求出
,求出![]() 的解,解不等式
的解,解不等式![]() ,即可得出結論;
,即可得出結論;
(2)函數![]() 有兩個極值點,即
有兩個極值點,即![]() 有兩個不同的解,分離參數,轉化為兩個函數交點,即可求解.
有兩個不同的解,分離參數,轉化為兩個函數交點,即可求解.
(1)![]() ,
,
直線![]() 的斜率為
的斜率為![]() ,
,
依題意有![]() ,
,
![]() ,設
,設![]() ,
,
當![]() 時,
時,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() 單調遞減,
單調遞減,
所以![]() 時,
時,![]() 取得極小值
取得極小值![]() ,也是最小值,
,也是最小值,
![]() ,所以
,所以![]() 在
在![]() 單調遞增,
單調遞增,
![]() 單調遞增區間是
單調遞增區間是![]() ,無單調遞減區間;
,無單調遞減區間;
(2)函數![]() 有兩個極值點,
有兩個極值點,
![]() 有兩個不同的解,
有兩個不同的解,
![]() ,令
,令![]() ,
,
等價于![]() 與
與![]() 有兩個不同的交點,
有兩個不同的交點,
![]() ,
,
![]() ,
,
![]() 遞增區間時
遞增區間時![]() ,遞減區間時
,遞減區間時![]()
當![]() 時,
時,![]() 取得極大值,也是最大值為
取得極大值,也是最大值為![]() ,
,
且![]() 時,
時,![]() ,
,
所以當![]() 時,
時,![]() 與
與![]() 有兩個交點,
有兩個交點,
即![]() 兩個不同的解,
兩個不同的解,
所以函數![]() 有兩個極值點,實數
有兩個極值點,實數![]() 的取值范圍是
的取值范圍是![]() .
.



科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 為
為![]() 上位于第一象限的任意一點,過點
上位于第一象限的任意一點,過點![]() 的直線
的直線![]() 交
交![]() 于另一點
于另一點![]() ,交
,交![]() 軸的正半軸于點
軸的正半軸于點![]() .
.
(1)若當點![]() 的橫坐標為
的橫坐標為![]() ,且
,且![]() 為等邊三角形,求
為等邊三角形,求![]() 的方程;
的方程;
(2)對于(1)中求出的拋物線![]() ,若點
,若點![]() ,記點
,記點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,求證:點
,求證:點![]() 的坐標為
的坐標為![]() ,并求點
,并求點![]() 到直線
到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《基礎教育課程改革綱要(試行)》將“具有良好的心理素質”列入新課程的培養目標.為加強心理健康教育工作的開展,不斷提高學生的心理素質,九江市某校高二年級開設了《心理健康》選修課,學分為2分.學校根據學生平時上課表現給出“合格”與“不合格”兩種評價,獲得“合格”評價的學生給予50分的平時分,獲得“不合格”評價的學生給予30分的平時分,另外還將進行一次測驗.學生將以“平時分×40%+測驗分×80%”作為“最終得分”,“最終得分”不少于60分者獲得學分.
該校高二(1)班選修《心理健康》課的學生的平時份及測驗分結果如下:
測驗分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
平時分50分人數 | 0 | 3 | 4 | 4 | 2 | ||
平時分30分人數 | 1 | 0 | 0 |
(1)根據表中數據完成如下2×2列聯表,并分析是否有95%的把握認為這些學生“測驗分是否達到60分”與“平時分”有關聯?
選修人數 | 測驗分 達到60分 | 測驗分 未達到60分 | 合計 |
平時分50分 | |||
平時分30分 | |||
合計 |
(2)若從這些學生中隨機抽取1人,求該生獲得學分的概率.
附: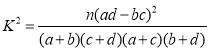 ,其中
,其中![]()
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為![]() .現有甲、乙兩人從袋中輪流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即終止.若摸出白球,則記2分,若摸出黑球,則記1分.每個球在每一次被取出的機會是等可能的.
.現有甲、乙兩人從袋中輪流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即終止.若摸出白球,則記2分,若摸出黑球,則記1分.每個球在每一次被取出的機會是等可能的.
(1)求袋中白球的個數;
(2)用表示甲,乙最終得分差的絕對值,求隨機變量![]() 的概率分布列及數學期望E
的概率分布列及數學期望E![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市調查機構在某設置過街天橋的路口隨機調查了110人準備過馬路的交通參與者對跨越護欄和走過街天橋的看法,得到如下列聯表:
男 | 女 | 合計 | |
走過街天橋 | 40 | 20 | 60 |
跨越護欄 | 20 | 30 | 50 |
合計 | 60 | 50 | 110 |
附:![]() .
.
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
則可以得到正確的結論是( )
A.有99%以上的把握認為“選擇過馬路的方式與性別有關”
B.有99%以上的把握認為“選擇過馬路的方式與性別無關”
C.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別有關”
D.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用1,2,3,4,5,6組成數字不重復的六位數,滿足1不在左右兩端,2,4,6三個偶數中有且只有兩個偶數相鄰,則這樣的六位數的個數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為積極響應國家“陽光體育運動”的號召,某學校在了解到學生的實際運動情況后,發起以“走出教室,走到操場,走到陽光”為口號的課外活動倡議,為調查該校學生每周平均體育運動時間的情況,從高一高二(非畢業年級)與高三(畢業年級)共三個年級學生中按照![]() 的比例分層抽樣,收集
的比例分層抽樣,收集![]() 位學生每周平均體育運動時間的樣本數據(單位:小時),得到如圖所示的頻率分布直方圖.(已知高一年級共有
位學生每周平均體育運動時間的樣本數據(單位:小時),得到如圖所示的頻率分布直方圖.(已知高一年級共有![]() 名學生)
名學生)
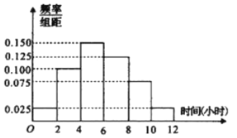
(1)據圖估計該校學生每周平均體育運動時間,并估計高一年級每周平均體育運動時間不足![]() 小時的人數;
小時的人數;
(2)規定每周平均體育運動時間不少于![]() 小時記為“優秀”,否則為“非優秀”,在樣本數據中,有
小時記為“優秀”,否則為“非優秀”,在樣本數據中,有![]() 位高三學生的每周平均體育運動時間不少于
位高三學生的每周平均體育運動時間不少于![]() 小時,請完成下列
小時,請完成下列![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“該校學生的每周平均體育運動時間是否優秀與畢業年級有關”?
的把握認為“該校學生的每周平均體育運動時間是否優秀與畢業年級有關”?
非畢業年級 | 畢業年級 | 合計 | |
優秀 | |||
非優秀 | |||
合計 |
|
附: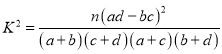 .
.
參考數據:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,-2),橢圓E: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F是橢圓E的右焦點,直線AF的斜率為
,F是橢圓E的右焦點,直線AF的斜率為![]() ,O為坐標原點.
,O為坐標原點.
(1)求E的方程;
(2)設過點A的動直線l與E相交于P,Q兩點.當△OPQ的面積最大時,求l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com