
分析 由△AF1F2是等腰直角三角形,可得b=c,可設橢圓的標準方程為:$\frac{{x}^{2}}{{2b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>0).在Rt△ABF1中,由勾股定理可得:丨AF1丨2+|AB|2=丨F2B丨2,|AF2|=|AF1|=$\sqrt{2}$b,設|BF2|=m,則|BF1|=2a-m=2$\sqrt{2}$b-m,2b2+($\sqrt{2}$b+m)2=(2$\sqrt{2}$b-m)2,又S=$\frac{1}{2}$丨AF1丨•丨AB丨=$\frac{1}{2}$×$\sqrt{2}$($\sqrt{2}$b+m)=8,聯立解出即可得出b2,即可求得橢圓C的標準方程.
解答 解:∵△AF1F2是等腰直角三角形,b=c,
可設橢圓的標準方程為:$\frac{{x}^{2}}{{2b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>0).
在Rt△ABF1中,由勾股定理可得:丨AF1丨2+|AB|2=丨F2B丨2,
|AF2|=|AF1|=$\sqrt{2}$b,設|BF2|=m,則|BF1|=2a-m=2$\sqrt{2}$b-m,
代入可得:2b2+($\sqrt{2}$b+m)2=(2$\sqrt{2}$b-m)2,
又△AF1B的面積S=$\frac{1}{2}$丨AF1丨•丨AB丨=$\frac{1}{2}$×$\sqrt{2}$($\sqrt{2}$b+m)=8,
聯立解得:b2=6,
∴橢圓的標準方程為:$\frac{x^2}{{{{12}^{\;}}}}+\frac{y^2}{6}=1$.
故答案為:$\frac{x^2}{{{{12}^{\;}}}}+\frac{y^2}{6}=1$.
點評 本題考查了橢圓的定義標準方程及其性質、勾股定理、三角形的面積計算公式,考查了推理能力與計算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
| 性別 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$-3 | B. | 2$\sqrt{2}$-1 | C. | 2$\sqrt{2}$+3 | D. | 2$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 課程 | 數學1 | 數學2 | 數學3 | 數學4 | 數學5 | 合計 |
| 選課人數 | 180 | 540 | 540 | 360 | 180 | 1800 |
查看答案和解析>>
科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(理)試卷(解析版) 題型:解答題
已知函數 ,
, ,(
,(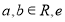 為自然對數的底數),且曲線
為自然對數的底數),且曲線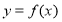 與
與 在坐標原點處的切線相同.
在坐標原點處的切線相同.
(1)求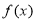 的最小值;
的最小值;
(2)若 時,
時, 恒成立,試求實數
恒成立,試求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com