(n=3,4,…).(1)求c的值;
(2)求數列{nan}的前n項和Sn.
分析:(2)c的取值不同Sn的結果不一樣,故需討論.
解:(1)由題設,當n≥3時,an=c2an-2,an-1=can-2,an==
an-2.由題設條件可得an-2≠0,因此c2=
,即2c2-c-1=0.解得c=1或c=-
.
(2)由(1),需要分兩種情況討論.當c=1時,數列{an}是一個常數列,即an=1(n∈N*).這時,數列{nan}的前n項和Sn=1+2+3+…+n=
.當c=-
時,數列{an}是一個公比為-
的等比數列,即an=(-
)n-1(n∈N*).這時,數列{nan}的前n項和Sn=1+2(-
)+3(-
)2+…+n(-
)n-1①,①式兩邊同乘-
,得-
Sn=-
+2(-
)2+…+(n-1)(-
)n-1+n(-
)n②,①式減去②式,得(1+
)Sn=1+(-
)+(-
)+(-
)2+…+(-
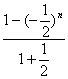)n-1-n(-
)n=
-n(-
)n.
所以Sn=
［4-(-1)n
］(n∈N*).
名校課堂系列答案科目：高中數學 來源： 題型：
| an-1+an-2 | 2 |
查看答案和解析>>
科目：高中數學 來源：天津 題型：解答題
| an-1+an-2 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
(n=3,4,…).