Question

8．拋物線y²=x與直線x-2y-3=0的兩個交點分別為P、Q，點M在拋物線上從P向Q運動（點M不同于點P、Q），
（Ⅰ）求由拋物線y²=x與直線x-2y-3=0所圍成的封閉圖形面積；
（Ⅱ）求使△MPQ的面積為最大時M點的坐標．

Answer 1

分析 （Ⅰ）由$\left\{\begin{array}{l}{y^2}=x\\ x-2y-3=0\end{array}\right.$得拋物線與直線的交點為P，Q，根據定積分的即可求出相對應的面積，方法一，選取積分變量為x，方法二，選取積分變量為y
（Ⅱ）設點M的坐標為（a，b），要使△MPQ的面積最大即使點M到直線x-2y-3=0的距離最大，故過點M的切線與直線x-2y-3=0平行，利用導數求出切線的斜率，即可求出a的值，問題得以解決．

解答 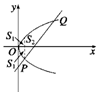解  （Ⅰ）方法一  由$\left\{\begin{array}{l}{y^2}=x\\ x-2y-3=0\end{array}\right.$得拋物線與直線的交點為P（1，-1），Q（9，3）（如圖）．
∴S=${∫}_{0}^{1}$[$\sqrt{x}$-（-$\sqrt{x}$）]dx+${∫}_{1}^{9}$（$\sqrt{x}$-$\frac{x-3}{2}$）dx=2${∫}_{0}^{1}$$\sqrt{x}$dx+${∫}_{1}^{9}$（$\sqrt{x}$-$\frac{x}{2}$+$\frac{3}{2}$）dx
=$\frac{4}{3}$$\sqrt{x^3}$|${\;}_{0}^{1}$+（$\frac{2}{3}$x${\;}^{\frac{3}{2}}$-$\frac{x^2}{4}$+$\frac{3}{2}x$|${\;}_{1}^{9}$=$\frac{4}{3}$+$\frac{28}{3}$=$\frac{32}{3}$．
方法二  若選取積分變量為y，則兩個函數分別為x=y²，x=2y+3．由方法一知上限為3，下限為-1．
∴S=${∫}_{-1}^{3}$（2y+3-y²）dy=（y²+3y-$\frac{1}{3}$y³）|${\;}_{-1}^{3}$=（9+9-9）-（1-3+$\frac{1}{3}$）=$\frac{32}{3}$．
（Ⅱ）設點M的坐標為（a，b），要使△MPQ的面積最大即使點M到直線x-2y-3=0的距離最大，
故過點M的切線與直線x-2y-3=0平行，
故過點M的切線斜率為k=$\frac{1}{2}$，
∵y²=x，
∴y=$\sqrt{x}$
令y=$\sqrt{x}$，
∴y′=$\frac{1}{2\sqrt{x}}$
∴k=$\frac{1}{2\sqrt{a}}$=$\frac{1}{2}$，
解得a=1，
∴b=1，
∴M點的坐標為（1，1）時，△PAB的面積最大．

點評 本題考查了定積分的有關計算和拋物線的簡單性質，以及導數的幾何意義，屬于中檔題．