
【題目】設a∈R,函數f(x)=x2e1﹣x﹣a(x﹣1).
(1)當a=1時,求f(x)在( ![]() ,2)內的極大值;
,2)內的極大值;
(2)設函數g(x)=f(x)+a(x﹣1﹣e1﹣x),當g(x)有兩個極值點x1 , x2(x1<x2)時,總有x2g(x1)≤λf′(x1),求實數λ的值.(其中f′(x)是f(x)的導函數.)
【答案】
(1)解:當a=1時,f(x)=x2e1﹣x﹣(x﹣1),則f'(x)=(2x﹣x2)e1﹣x﹣1= ![]() ,
,
令h(x)=(2x﹣x2)﹣ex﹣1,則h'(x)=2﹣2x﹣ex﹣1,
顯然h'(x)在( ![]() ,2)內是減函數,
,2)內是減函數,
又因h'( ![]() )=
)= ![]() <0,故在(
<0,故在( ![]() ,2)內,總有h'(x)<0,
,2)內,總有h'(x)<0,
∴h(x)在( ![]() ,2)上是減函數,
,2)上是減函數,
又因h(1)=0,
∴當x∈( ![]() ,1)時,h(x)>0,從而f'(x)>0,這時f(x)單調遞增,
,1)時,h(x)>0,從而f'(x)>0,這時f(x)單調遞增,
當x∈(1,2)時,h(x)<0,從而f'(x)<0,這時f(x)單調遞減,
∴f(x)在( ![]() ,2)的極大值是f(1)=1.
,2)的極大值是f(1)=1.
(2)解:由題意可知g(x)=(x2﹣a)e1﹣x,則g'(x)=(2x﹣x2+a)e1﹣x=(﹣x2+2x+a)e1﹣x.
根據題意,方程﹣x2+2x+a=0有兩個不同的實根x1,x2(x1<x2),
∴△=4+4a>0,即a>﹣1,且x1+x2=2,∵x1<x2,∴x1<1.
由x2g(x1)≤λf′(x1),其中f'(x)=(2x﹣x2)e1﹣x﹣a,
可得(2﹣x1)( ![]() )
) ![]() ,
,
注意到 ![]() ,
,
∴上式化為(2﹣x1)(2x1) ![]() ,
,
即不等式 ![]() ≤0對任意的x1∈(﹣∞,1)恒成立,
≤0對任意的x1∈(﹣∞,1)恒成立,
(i)當x1=0時,不等式 ![]() ≤0恒成立,λ∈R;
≤0恒成立,λ∈R;
(ii)當x1∈(0,1)時, ![]() 恒成立,即
恒成立,即 ![]() .
.
令函數k(x)= ![]() =2﹣
=2﹣ ![]() ,顯然,k(x)是R上的減函數,
,顯然,k(x)是R上的減函數,
∴當x∈(0,1)時,k(x)<k(0)= ![]() ,∴
,∴ ![]() ;
;
(iii)當x1∈(﹣∞,0)時, ![]() ≥0恒成立,即
≥0恒成立,即 ![]() .
.
由(ii),當x∈(﹣∞,0)時,k(x)>k(0)= ![]() ,∴
,∴ ![]() ;
;
綜上所述, ![]() .
.
【解析】(1)當a=1時,可求得f'(x)= ![]() ,令h(x)=(2x﹣x2)﹣ex﹣1 , 利用導數可判斷h(x)的單調性并得其零點,從而可得原函數的極值點及極大值;(2)表示出g(x),并求得g'(x)=(﹣x2+2x+a)e1﹣x , 由題意,得方程﹣x2+2x+a=0有兩個不同的實根x1 , x2(x1<x2),從而可得△=4+4a>0及x1+x2=2,由x1<x2 , 得x1<1.則x2g(x1)≤λf′(x1)可化為
,令h(x)=(2x﹣x2)﹣ex﹣1 , 利用導數可判斷h(x)的單調性并得其零點,從而可得原函數的極值點及極大值;(2)表示出g(x),并求得g'(x)=(﹣x2+2x+a)e1﹣x , 由題意,得方程﹣x2+2x+a=0有兩個不同的實根x1 , x2(x1<x2),從而可得△=4+4a>0及x1+x2=2,由x1<x2 , 得x1<1.則x2g(x1)≤λf′(x1)可化為 ![]() ≤0對任意的x1∈(﹣∞,1)恒成立,按照x1=0、x1∈(0,1)、x1∈(﹣∞,0)三種情況分類討論,分離參數λ后轉化為求函數的最值可解決;
≤0對任意的x1∈(﹣∞,1)恒成立,按照x1=0、x1∈(0,1)、x1∈(﹣∞,0)三種情況分類討論,分離參數λ后轉化為求函數的最值可解決;
【考點精析】本題主要考查了函數的極值與導數和函數的最大(小)值與導數的相關知識點,需要掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值;求函數
是極小值;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.
比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=(﹣x2+ax﹣3)ex(a為實數).
(1)當a=4時,求函數y=g(x)在x=0處的切線方程;
(2)求f(x)在區間[t,t+2](t>0)上的最小值;
(3)如果關于x的方程g(x)=2exf(x)在區間[ ![]() ,e]上有兩個不等實根,求實數a的取值范圍.
,e]上有兩個不等實根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1、F2分別是雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右焦點,若在雙曲線的右支上存在一點M,使得(
=1(a>0,b>0)的左右焦點,若在雙曲線的右支上存在一點M,使得( ![]() +
+ ![]() )
) ![]() =0(其中O為坐標原點),且|
=0(其中O為坐標原點),且| ![]() |=
|= ![]() |
| ![]() |,則雙曲線離心率為 .
|,則雙曲線離心率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x),若a,b,c∈R,f(a),f(b),f(c)為某一三角形的三邊長,則稱f(x)為“可構造三角形函數”.已知函數f(x)=![]() 是“可構造三角形函數”,則實數t的取值范圍是( )
是“可構造三角形函數”,則實數t的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為調查高二學生上學路程所需要的時間(單位:分鐘),從高二年級學生中隨機抽取![]() 名按上學所需要時間分組:第
名按上學所需要時間分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
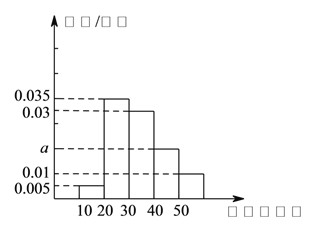
(![]() )根據圖中數據求
)根據圖中數據求![]() 的值.
的值.
(![]() )若從第
)若從第![]() ,
, ![]() ,
, ![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名新生參與交通安全問卷調查,應從第
名新生參與交通安全問卷調查,應從第![]() ,
, ![]() ,
, ![]() 組各抽取多少名新生?
組各抽取多少名新生?
(![]() )在(
)在(![]() )的條件下,該校決定從這
)的條件下,該校決定從這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名新生參加交通安全宣傳活動,求第
名新生參加交通安全宣傳活動,求第![]() 組至少有一志愿者被抽中的概率.
組至少有一志愿者被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 圓![]() ,過點
,過點![]() 作圓
作圓![]() 的切線,切點分別為
的切線,切點分別為![]() 、
、![]() ,且
,且![]() (
(![]() 為原點).
為原點).
(![]() )求點
)求點![]() 的軌跡方程.
的軌跡方程.
(![]() )求四邊形
)求四邊形![]() 面積的最小值.
面積的最小值.
(![]() )設
)設![]() ,
, ![]() ,在圓
,在圓![]() 上存在點
上存在點![]() ,使得
,使得![]() ,求
,求![]() 的最大值和最小值(直接寫出結果即可).
的最大值和最小值(直接寫出結果即可).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x2﹣2ax+b|(x∈R),給出下列命題:
①a∈R,使f(x)為偶函數;
②若f(0)=f(2),則f(x)的圖象關于x=1對稱;
③若a2﹣b≤0,則f(x)在區間[a,+∞)上是增函數;
④若a2﹣b﹣2>0,則函數h(x)=f(x)﹣2有2個零點.
其中正確命題的序號為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com