
【題目】已知數列![]() 的首項
的首項![]() (
(![]() 是常數,且
是常數,且![]() ),
),![]()
![]() ,數列
,數列![]() 的首項
的首項![]() ,
,![]()
![]() .
.
(1)證明:![]() 從第2項起是以2為公比的等比數列;
從第2項起是以2為公比的等比數列;
(2)設![]() 為數列
為數列![]() 的前
的前![]() 項和,且
項和,且![]() 是等比數列,求實數
是等比數列,求實數![]() 的值;
的值;
(3)當![]() 時,求數列
時,求數列![]() 的最小項.
的最小項.
【答案】(1)證明見解析;(2)![]() ;
;
(3)當![]() 時,最小項為
時,最小項為![]() ;
;
當![]() 時,最小項為
時,最小項為![]() 或
或![]() ;
;
當![]() 時,最小項為
時,最小項為![]() ;
;
當![]() 時,最小項為
時,最小項為![]() 或
或![]() ;
;
當![]() 時,最小項為
時,最小項為![]() .
.
【解析】
(1)對![]() 進行化簡,代入
進行化簡,代入![]() ,然后得到與
,然后得到與![]() 的關系,得到
的關系,得到![]() 從第2項起是以2為公比的等比數列;(2)先得到
從第2項起是以2為公比的等比數列;(2)先得到![]() 的表達式,然后得到
的表達式,然后得到![]() ,根據
,根據![]() 是等比數列,得到
是等比數列,得到![]() 的方程,求出
的方程,求出![]() 的值;(3)根據得到的
的值;(3)根據得到的![]() 的通項,分類討論,得到
的通項,分類討論,得到![]() 中的最小項.
中的最小項.
解:(1)![]()
![]()
![]()
![]()
![]()
由![]() ,得
,得![]() ,
,![]()
![]() ,
,![]()
即![]() 從第2項起是以2為公比的等比數列.
從第2項起是以2為公比的等比數列.
(2)![]()
![]()
當![]() 時,
時,![]()
![]()
![]() 是等比數列,
是等比數列,
![]() 是常數,
是常數,![]() ,
,
即![]()
(3)由(1)知當![]() 時,
時,![]() ,
,
所以![]() ,
,
所以數列![]() 為
為![]()
顯然最小項是前三項中的一項.
當![]() 時,最小項為
時,最小項為![]() ;
;
當![]() 時,最小項為
時,最小項為![]() 或
或![]() ;
;
當![]() 時,最小項為
時,最小項為![]() ;
;
當![]() 時,最小項為
時,最小項為![]() 或
或![]() ;
;
當![]() 時,最小項為
時,最小項為![]() .
.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:
【題目】房屋的天花板上點![]() 處有一光源,
處有一光源,![]() 在地面上的射影為
在地面上的射影為![]() ,在地面上放置正棱錐
,在地面上放置正棱錐![]() ,底面
,底面![]() 接觸地面.已知正四棱錐
接觸地面.已知正四棱錐![]() 的高為
的高為![]() ,底面
,底面![]() 的邊長為
的邊長為![]() ,
,![]() 與正方形
與正方形![]() 的中心
的中心![]() 的距離為
的距離為![]() ,又
,又![]() 長為
長為![]() ,則棱錐影子(不包括底面
,則棱錐影子(不包括底面![]() )的面積的最大值為________.
)的面積的最大值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,
中,![]() ,若
,若![]() (
(![]() 為常數),則稱
為常數),則稱![]() 為“等差比數列”.下列是對“等差比數列”的判斷:
為“等差比數列”.下列是對“等差比數列”的判斷:
①![]() 不可能為
不可能為![]() ;②等差數列一定是等差比數列;
;②等差數列一定是等差比數列;
③等比數列一定是等差比數列;④等差比數列中可以有無數項為![]() .
.
其中正確的判斷是( ).
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015全國高考試題)某公司為了解用戶對其產品的滿意度,從![]() ,
,![]() 兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
![]() 地區:62 73 81 92 95 85 74 64 53 76
地區:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
![]() 地區:73 83 62 51 91 46 53 73 64 82
地區:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
根據用戶滿意度評分,將用戶的滿意度從低到高分為三個不同等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
記事件![]() :“
:“![]() 地區用戶的滿意度等級高于
地區用戶的滿意度等級高于![]() 地區用戶的滿意度等級”假設兩地區用戶的評價結果相互獨立.根據所給數據,以事件發生的頻率作為相應事件發生的概率,求
地區用戶的滿意度等級”假設兩地區用戶的評價結果相互獨立.根據所給數據,以事件發生的頻率作為相應事件發生的概率,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年4月8日零時正式解除離漢通道管控,這標志著封城76天的武漢打開城門了.在疫情防控常態下,武漢市有序復工復產復市,但是仍然不能麻痹大意,仍然要保持警惕,嚴密防范、慎終如始.為科學合理地做好小區管理工作,結合復工復產復市的實際需要,某小區物業提供了![]() ,
,![]() 兩種小區管理方案,為了了解哪一種方案最為合理有效,物業隨機調查了50名男業主和50名女業主,每位業主對
兩種小區管理方案,為了了解哪一種方案最為合理有效,物業隨機調查了50名男業主和50名女業主,每位業主對![]() ,
,![]() 兩種小區管理方案進行了投票(只能投給一種方案),得到下面的列聯表:
兩種小區管理方案進行了投票(只能投給一種方案),得到下面的列聯表:
|
| |
男業主 | 35 | 15 |
女業主 | 25 | 25 |
(1)分別估計![]() ,
,![]() 方案獲得業主投票的概率;
方案獲得業主投票的概率;
(2)判斷能否有95%的把握認為投票選取管理方案與性別有關.
附: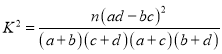 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的各項均為正數,其前n項的積為
的各項均為正數,其前n項的積為![]() ,記
,記![]() ,
,![]() .
.
(1)若數列![]() 為等比數列,數列
為等比數列,數列![]() 為等差數列,求數列
為等差數列,求數列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求數列![]() 的通項公式.
的通項公式.
②記![]() ,那么數列
,那么數列![]() 中是否存在兩項
中是否存在兩項![]() ,(s,t均為正偶數,且
,(s,t均為正偶數,且![]() ),使得數列
),使得數列![]() ,
,![]() ,
,![]() ,成等差數列?若存在,求s,t的值;若不存在,請說明理由.
,成等差數列?若存在,求s,t的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com