
【題目】已知雙曲線![]() 的離心率為2,
的離心率為2,![]() 分別是雙曲線的左、右焦點,點
分別是雙曲線的左、右焦點,點![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 上的動點,當
上的動點,當![]() 取得最小值和最大值時,
取得最小值和最大值時,![]() 的面積分別為
的面積分別為![]() ,則
,則![]() ____________.
____________.
【答案】![]()
【解析】
利用雙曲線的離心率推出b=![]() a,線段MN所在直線的方程為y=
a,線段MN所在直線的方程為y=![]() (x+a),點P在線段MN上,可設P(m,
(x+a),點P在線段MN上,可設P(m,![]() (m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通過斜率的數量積求出
(m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通過斜率的數量積求出![]() 的最值,然后求解結果.
的最值,然后求解結果.
由已知e=![]() =2得c=2a,b=
=2得c=2a,b=![]() a,故線段MN所在直線的方程為y=
a,故線段MN所在直線的方程為y=![]() (x+a),又點P在線段MN上,可設P(m,
(x+a),又點P在線段MN上,可設P(m,![]() (m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得
(m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得![]() =(2am,
=(2am,![]() (m+a)),
(m+a)),![]() (2am,
(2am,![]() (m+a))),則
(m+a))),則![]() 4m2+6am
4m2+6am![]() ,由m∈[-a,0],可知當m=-
,由m∈[-a,0],可知當m=-![]() a時,
a時,![]() 取得最小值,此時S1=
取得最小值,此時S1=![]() ×2c×
×2c×![]() (-
(-![]() a+a)=
a+a)=![]() ac,當m=0時,
ac,當m=0時,![]() 取得最大值,此時S2=
取得最大值,此時S2=![]() ×2c×
×2c×![]() a=
a=![]()
ac,所以![]()
![]() .
.
故答案為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知x,y∈R,且 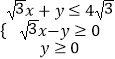 ,則存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)構成的區域面積為( )
,則存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)構成的區域面積為( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 點(n,Sn+3)(n∈N*)在函數y=3×2x的圖象上,等比數列{bn}滿足bn+bn+1=an(n∈N*).其前n項和為Tn , 則下列結論正確的是( )
A.Sn=2Tn
B.Tn=2bn+1
C.Tn>an
D.Tn<bn+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位打字員在兩臺電腦上各自輸入A,B兩種類型的文件的部分文字才能使這兩類文件成為成品.已知A文件需要甲輸入0.5小時,乙輸入0.2小時;B文件需要甲輸入0.3小時,乙輸入0.6小時.在一個工作日中,甲至多只能輸入6小時,乙至多只能輸入8小時,A文件每份的利潤為60元,B文件每份的利潤為80元,則甲、乙兩位打字員在一個工作日內獲得的最大利潤是元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣2|+|x+4|,g(x)=x2+4x+3.
(1)求不等式f(x)≥g(x)的解集;
(2)若f(x)≥|1﹣5a|恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分8分)某班50名學生在一次數學測試中,成績全部介于50與100之間,將測試結果按如下方式分成五組:第一組[50,60),第二組[60,70),…,第五組[90,100].如圖所示是按上述分組方法得到的頻率分布直方圖.

(Ⅰ)若成績大于或等于60且小于80,認為合格,求該班在這次數學測試中成績合格的人數;
(Ⅱ)從測試成績在[50,60)∪[90,100]內的所有學生中隨機抽取兩名同學,設其測試成績分別為m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (x>0),m∈R.
(x>0),m∈R.
(1)若函數f(x)有零點,求實數m的取值范圍;
(2)若函數f(x)的圖象在點(1,f(x))處的切線的斜率為 ![]() ,且函數f(x)的最大值為M,求證:1<M<
,且函數f(x)的最大值為M,求證:1<M< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】祖暅(公元前5~6世紀)是我國齊梁時代的數學家,是祖沖之的兒子.他提出了一條原理:“冪勢既同,則積不容異.”這里的“冪”指水平截面的面積,“勢”指高.這句話的意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體體積相等.設由橢圓 ![]() =1(a>b>0)所圍成的平面圖形繞y軸旋轉一周后,得一橄欖狀的幾何體(如圖)(稱為橢球體),課本中介紹了應用祖暅原理求球體體積公式的做法,請類比此法,求出橢球體體積,其體積等于 .
=1(a>b>0)所圍成的平面圖形繞y軸旋轉一周后,得一橄欖狀的幾何體(如圖)(稱為橢球體),課本中介紹了應用祖暅原理求球體體積公式的做法,請類比此法,求出橢球體體積,其體積等于 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ax﹣lnx(a∈R,a為常數)
(1)當a=﹣1時,若方程f(x)= ![]() 有實根,求b的最小值;
有實根,求b的最小值;
(2)設F(x)=f(x)e﹣x , 若F(x)在區間(0,1]上是單調函數,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com