
【題目】已知數列{an}的前n項和為Sn , 且滿足a1=1,anan+1=2Sn , 設bn= ![]() ,若存在正整數p,q(p<q),使得b1 , bp , bq成等差數列,則p+q= .
,若存在正整數p,q(p<q),使得b1 , bp , bq成等差數列,則p+q= .
【答案】5
【解析】解:數列{an}滿足a1=1,anan+1=2Sn , ∴n=1時,a1a2=2S1=2a1 , 解得a2=2.n≥2時,2an=2(Sn﹣Sn﹣1)=an(an+1﹣an﹣1),∵an≠0,∴an+1﹣an﹣1=2. ∴數列{an}是首項為1,公差為1的等差數列,∴an=1+n﹣1=n.
∴bn= ![]() =
= ![]() .
.
∵存在正整數p,q(p<q),使得b1 , bp , bq成等差數列,
∴2bp=b1+bq , ∴ ![]() =
= ![]() (*).
(*).
∵數列{bn}是單調遞減數列.
當p=1時,由 ![]() +
+ ![]() ,解得q=1,舍去.
,解得q=1,舍去.
當2≤p<q時, ![]() ,
, ![]() ﹣
﹣ ![]() =
= ![]() .
.
當3≤p時, ![]() ≥
≥ ![]() ,
, ![]() >0,∴
>0,∴ ![]() +
+ ![]() ,(*)不成立.
,(*)不成立.
∴p=2,可得: ![]() =
= ![]() +
+ ![]() ,解得q=3.
,解得q=3.
∴p+q=5.
【考點精析】認真審題,首先需要了解數列的前n項和(數列{an}的前n項和sn與通項an的關系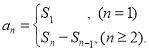 ).
).


科目:高中數學 來源: 題型:
【題目】已知動點M(x,y)到直線l:x=3的距離是它到點D(1,0)的距離的 ![]() 倍.
倍.
(1)求動點M的軌跡C的方程;
(2)設軌跡C上一動點T滿足: ![]() =2λ
=2λ ![]() +3μ
+3μ ![]() ,其中P、Q是軌跡C上的點,且直線OP與OQ的斜率之積為﹣
,其中P、Q是軌跡C上的點,且直線OP與OQ的斜率之積為﹣ ![]() .若N(λ,μ)為一動點,F1(﹣
.若N(λ,μ)為一動點,F1(﹣ ![]() ,0)、F2(
,0)、F2( ![]() ,0)為兩定點,求|NF1|+|NF2|的值.
,0)為兩定點,求|NF1|+|NF2|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】辦公室裝修一新,放些植物花草可以清除異味,公司提供綠蘿、文竹、碧玉、蘆薈4種植物供員工選擇,每個員工任意選擇2種,則員工甲和乙選擇的植物全不同的概率為:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】意大利著名數學家斐波那契在研究兔子的繁殖問題時,發現有這樣的一列數:1,1,2,3,5,8,…,該數列的特點是:前兩個數均為1,從第三個數起,每一個數都等于它前面兩個數的和.人們把這樣的一列數組成的數列{an}稱為斐波那契數列,則 ![]() ﹣
﹣ ![]() =( )
=( )
A.0
B.﹣1
C.1
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]()
(1)求圓![]() 關于直線
關于直線![]() 對稱的圓
對稱的圓![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 被圓
被圓![]() 截得的弦長為8,求直線
截得的弦長為8,求直線![]() 的方程;
的方程;
(3)當![]() 取何值時,直線
取何值時,直線![]() 與圓
與圓![]() 相交的弦長最短,并求出最短弦長.
相交的弦長最短,并求出最短弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃在甲、乙兩個電視臺做總時間不超過300分鐘的廣告,廣告費用不超過9萬元,甲、乙電視臺的廣告費標準分別是500元/分鐘和200元分鐘,假設甲、乙兩個電視臺為該公司做的廣告能給公司帶來的收益分別為0.4萬元/分鐘和0.2萬元分鐘,那么該公司合理分配在甲、乙兩個電視臺的廣告時間,能使公司獲得最大的收益是()萬元
A.72B.80C.84D.90
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,為了測量A,B處島嶼的距離,小明在D處觀測,A,B分別在D處的北偏西15°、北偏東45°方向,再往正東方向行駛40海里至C處,觀測B在C處的正北方向,A在C處的北偏西60°方向,則A,B兩處島嶼間的距離為( ) 
A.![]() 海里
海里
B.![]() 海里
海里
C.![]() 海里
海里
D.40海里
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com