將與105互素的所有正整數從小到大排成數列,試求出這個數列的第1000項.
【答案】
分析:由105=3×5×7,知不超過105而與105互質的正整數有48個.由此能求出這個數列的第1000項.
解答:解:由105=3×5×7,
由容斥原理,每連續105個數中,
有105-(
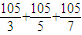
)+
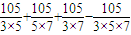
=105×(1-

)(1-
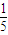
)(1-

)=48,
故不超過105而與105互質的正整數有48個.
1000=48×20+48-8,
105×20=2100.
自105向前倒數,第9個與105互素的數是86,
∴在不超過105的與105互質的數中第40個數是86.
∴所求數為2100+86=2186.
故這個數列的第1000項是2186.
點評:本題考查數列的應用,解題時要認真審題,仔細解答,注意等價轉化思想的合理運用.

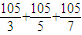 )+
)+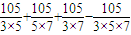
 )(1-
)(1-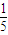 )(1-
)(1- )=48,
)=48,
