
在數列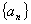 中,
中,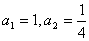 ,且
,且 .
.
(Ⅰ) 求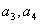 ,猜想
,猜想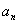 的表達式,并加以證明;
的表達式,并加以證明;
(Ⅱ)設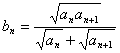 ,求證:對任意的自然數
,求證:對任意的自然數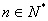 都有
都有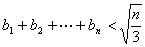 .
.
(Ⅰ) 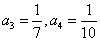 ,
,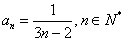 (Ⅱ)
(Ⅱ)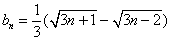
所以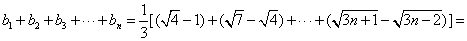
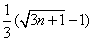 所以只需要證明
所以只需要證明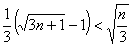
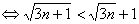
 (顯然成立),所以命題得證
(顯然成立),所以命題得證
解析試題分析:(Ⅰ)容易求得: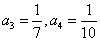 . 1分
. 1分
故可以猜想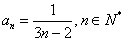 .下面利用數學歸納法加以證明:
.下面利用數學歸納法加以證明:
顯然當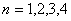 時,結論成立. 2分
時,結論成立. 2分
假設當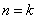 ;
; 時(也可以
時(也可以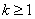 ),結論也成立,即
),結論也成立,即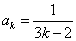 ,
,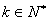 . 3分
. 3分
那么當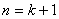 時,由題設與歸納假設可知:
時,由題設與歸納假設可知: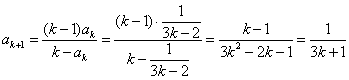
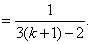 4分
4分
即當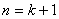 時,結論也成立,綜上,對
時,結論也成立,綜上,對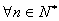 ,
,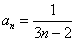 成立. 6分
成立. 6分
(Ⅱ)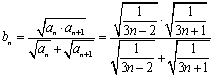
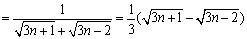 , 8分
, 8分
所以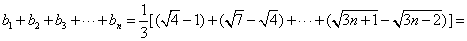
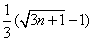 . 10分
. 10分
所以只需要證明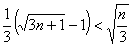
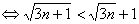
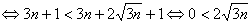 (顯然成立)
(顯然成立)
所以對任意的自然數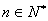 ,都有
,都有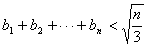 . 12分
. 12分
考點:數學歸納法及數列求和
點評:數學歸納法用來證明與正整數有關的題目,證明步驟:1,證明當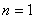 時命題成立。2,假設當
時命題成立。2,假設當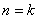 時命題成立,借此證明當
時命題成立,借此證明當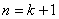 是命題成立,綜上1,2得證;數列求和常用的方法有分組求和裂項相消求和錯位相減求和等
是命題成立,綜上1,2得證;數列求和常用的方法有分組求和裂項相消求和錯位相減求和等


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)=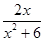 .
.
(1)若f(x)>k的解集為{x|x<-3,或x>-2},求k的值;
(2)對任意x>0,f(x)≤t恒成立,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
交通管理部門為了優化某路段的交通狀況,經過對該路段的長期觀測發現:在交通繁忙的時段內,該路段內汽車的車流量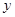 (千輛/時)與汽車的平均速度
(千輛/時)與汽車的平均速度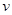 (千米/時)之間的函數關系為
(千米/時)之間的函數關系為
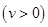
①求在該路段內,當汽車的平均速度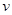 為多少時,車流量最大?最大車流量為多少?(精確到
為多少時,車流量最大?最大車流量為多少?(精確到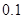 千輛/時)
千輛/時)
②若要求在該時段內車流量超過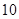 千輛/時,則汽車的平均速度應限定在什么范圍內?
千輛/時,則汽車的平均速度應限定在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知矩形ABCD,AB=8,BC=6,按以下兩種方法將其折疊為兩部分,設兩部分的面積為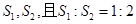 ,折痕為線段EF,問用哪一種方法折疊,折痕EF最長?并求EF長度的最大值.
,折痕為線段EF,問用哪一種方法折疊,折痕EF最長?并求EF長度的最大值.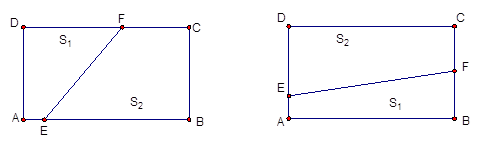
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com